Back to the Classics!
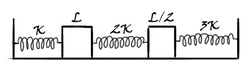 The above system comprises of three ideal springs, and two thick rods (they don't look like a rod!).The Temperature of the above system is increased by
. The coefficient of linear expansion of the material of the rods is
.
The above system comprises of three ideal springs, and two thick rods (they don't look like a rod!).The Temperature of the above system is increased by
. The coefficient of linear expansion of the material of the rods is
.
Calculate the energy stored in the spring with spring constant .
Details and Assumptions:
The springs are initially relaxed.
The rods expand only in the horizontal direction.
Neglect the expansion of the springs due to the increase in temperature
The answer is 0.000005355.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the compression in springs be x 1 , x 2 , and x 3 .
On balancing forces on rods,
x 1 = 2 x 2 = 3 x 3 .
Hence, x 1 = 2 x 2 , x 3 = 3 2 x 2
Now, the elongation of rods is balanced by compression of springs, hence,
x 1 + x 2 + x 3 = 2 3 L α △ T
Thus, x 2 = 2 2 9 L α △ T
Required energy stored = 2 1 2 K x 2 2 = K ( 2 2 9 L α △ T ) 2 ≈ 0 . 0 0 0 0 0 5 3 5 5