Bad Ineq 3

Algebra Level 4

Say we have 8 numbers, a , b , c , d , e , f , g , h {a,b,c,d,e,f,g,h} such that a b c d = 4 abcd=4 and e f g h = 9 efgh=9 . Find the minimum value of ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( d h ) 2 (ae)^2 + (bf)^2 + (cg)^2 + (dh)^2 .


The answer is 24.

View wiki
Josh Speckman by Josh Speckman , 20, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Mehul Chaturvedi
Jan 10, 2015

Please upvote if you like it

As we know A M ≥ G M AM \geq GM

⇒ ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( h d ) 2 4 ≥ ( a b c d e ) 2 4 \Rightarrow \dfrac{(ae)^2+(bf)^2+(cg)^2+(hd)^2}{4} \geq \sqrt [ 4 ]{(abcde)^2 }

Also a b c d e = 9 × 4 = 36 abcde=9\times 4=36

⇒ ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( h d ) 2 4 ≥ ( 36 ) 2 4 \Rightarrow \dfrac{(ae)^2+(bf)^2+(cg)^2+(hd)^2}{4} \geq \sqrt [ 4 ]{(36)^2 }

⇒ ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( h d ) 2 4 ≥ ( 6 ) 4 4 \Rightarrow \dfrac{(ae)^2+(bf)^2+(cg)^2+(hd)^2}{4} \geq \sqrt [ 4 ]{(6)^4 }

⇒ ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( h d ) 2 4 ≥ 6 \Rightarrow \dfrac{(ae)^2+(bf)^2+(cg)^2+(hd)^2}{4} \geq 6

⇒ ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( h d ) 2 ≥ 24 \Rightarrow (ae)^2+(bf)^2+(cg)^2+(hd)^2 \geq 24

Hence answer is ⇒ 24 \Huge\Rightarrow \color{royalblue}{\boxed{24}}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

You need to explain why you could use AM-GM when they are not strictly positive numbers.

Like the challenge master said, you should show that one of the terms could equal 0.

One easy way is to say that if a e = 0 ae=0 , then either a = 0 , e = 0 , a=0, e=0, or both equal 0. If a = 0 a=0 , then a b c d ≠ 4 abcd≠4 . If e = 0 e=0 , e f g h ≠ 9 efgh≠9 . This means that a e ≠ 0 ae≠0 .

Similarily, this works for a e , b f , c g ae, bf, cg , and h d hd . Now we can use AM-GM.

pickle lamborghini - 5 years, 7 months ago

Log in to reply

Not equal to 0 doesn't tell us that it is always greater than 0.

Satyajit Ghosh - 5 years, 6 months ago
Satvik Choudhary
Jun 8, 2015

By cauchy schwarz inequality [ ( a e ) 2 + ( b f ) 2 + ( c g ) 2 + ( d h ) 2 ] [ ( 1 a 2 + 1 b 2 + 1 c 2 + 1 d 2 ] > = [ e + f + g + h ] 2 [(ae)^{2}+(bf)^{2}+(cg)^{2}+(dh)^{2}][(\frac {1}{a^{2}}+\frac {1}{b^{2}}+\frac {1}{c^{2}}+\frac {1}{d^{2}}]>=[e+f+g+h]^{2}

2 Helpful 1 Interesting 0 Brilliant 0 Confused

You cannot get the answer from here. Its efgh=4.

Satyajit Ghosh - 5 years, 6 months ago
Vraj Mistry
May 23, 2015

I used Hit and Trial;My first thought came that all a,b,c,d would have the value of 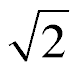and e,f,g,h would be 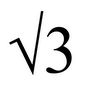; Thats it i replaced all values in the equation and found that answer is 24

0 Helpful 1 Interesting 1 Brilliant 0 Confused
Jyotsna Sharma
Jan 2, 2015

Using AM>=GM, We get that ((ae)^2+(be)^2+(cg)^2+(dh)^2)/4>=((abcdefgh)^2)^1/4=(36)^1/2=6 Therefore the least value of ((ae)^2+(be)^2+(cg)^2+(dh)^2)=6×4=24

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

You need to explain why you could use AM-GM when they are not strictly positive numbers.

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...