Baker's Parallax
A baker is cutting a loaf of bread. He has a slight error in his vision, so whenever he cuts the loaf in half it is in the ratio of 4 : 6 . He starts by cutting the bread into two pieces, then he cuts the two pieces in the same way of 4 : 6 and continues to do it a total of five times. What is the ratio of the smallest to the largest slice in the end?
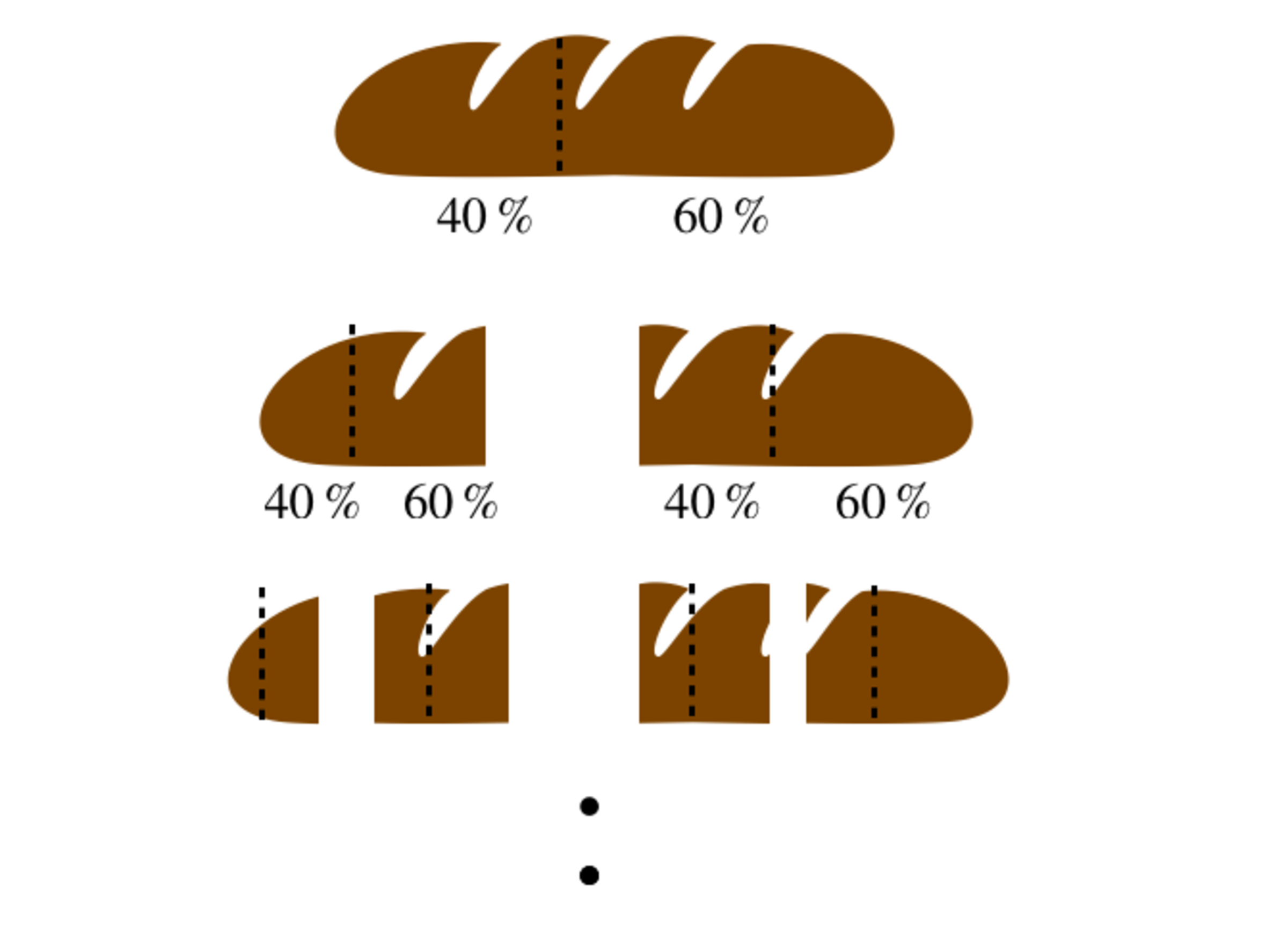
Note: For simplicity, assume that the bread is a perfect cuboid
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The ratio is of the form
0 . 4 n : 0 . 6 n
0 . 4 5 : 0 . 6 5 = 0 . 0 1 0 2 4 : 0 . 0 7 7 7 6 = 1 0 2 4 : 7 7 7 6
Quite easy.....
After each cut, the smallest piece of the loaf will be ( 1 0 0 4 0 ) t h or ( 5 2 ) t h of the previous one, and the largest will be ( 5 3 ) t h of the previous one. So, after n cuts, the smallest slice will be ( 5 n 2 n ) t h and the largest one will be ( 5 n 3 n ) t h of the original size of the loaf. Hence the required ratio is 3 n 2 n . For n = 5 , the ratio is 3 5 2 5 = 2 4 3 3 2 = 7 7 7 6 1 0 2 4
Let the volume of the loaf be 1 , x = 4 0 % = 0 . 4 and y = 6 0 % = 0 . 6 . Then after the first cut the two pieces are x : y . After the second cut x 2 : x y : y x : y 2 . Note that the sizes of the pieces follow binomial expansion ( x + y ) 1 = x + y , ( x + y ) 2 = x 2 + 2 x y + y 2 , ( x + y ) 3 .... Therefore after the fifth cut, we have ( x + y ) 5 = x 5 + 5 x 4 y + 1 0 x 3 y 2 + 1 0 x 2 y 3 + 5 x y 4 + y 5 . The smallest piece is x 5 and the largest y 5 . And their ratio is:
y 5 x 5 = ( 0 . 6 0 . 4 ) 5 = ( 6 4 ) 5 = 7 7 7 6 1 0 2 4 or 1 0 2 4 : 7 7 7 6