Balance a cart on an edge
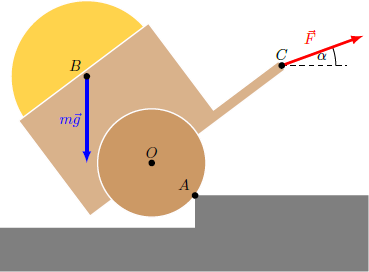
A one-axle cart balances on a step and is only supported by point on the ground. The axis is rotatably mounted at point . The center of gravity of the cart is at point .
What is the absolute value of the force that must be applied at point to hold the cart in place? In this case, the sum of all forces and torques acting on the cart must be zero.
Compare the force with the weight of the cart.
The points and are given by the position vectors (These numbers are given in decimeters.)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The points A , B and C each form, together with the origin O , right-angled triangles whose sides are in the ratio 5 : 4 : 3 .
In each of the points A , B and C a force acts on the car. In point B this is the weight with F B = ( 0 , − m g ) . The force at point A is exerted by the edge on the wheel. Since the wheel does not transmit torque to its axis (the wheel is rotatably mounted), the force acts along the connecting line between A and the origin. Therefore, the force vector can written as F A = ( − 5 4 , 5 3 ) F A . The force F = F C force at point C has an unknown angle α to the horizontal. Thus, the vector yields F C = ( cos α , sin α ) F C .
The sum of all forces must be zero:
⇒ 0 = i ∑ F i 0 m g = F A + F B + F C = ( − 5 4 F A 5 3 F A ) + ( 0 − m g ) + ( cos α F C sin α F C ) = − 5 4 F A + cos α F C = 5 3 F A + sin α F C ( I ) ( I I ) By multiplying the first line by the factor 3/4 and adding the two lines, the unknown F A can be eliminated: 4 3 ( I ) + ( I I ) = m g = ( 4 3 cos α + sin α ) F C ( I I I )
In addition, the total torque must be zero ⇒ 0 = i ∑ T i m g = A × F A + B × F B + C × F C = ⎝ ⎛ 4 − 3 0 ⎠ ⎞ × ⎝ ⎛ − 5 4 F A 5 3 F A 0 ⎠ ⎞ + ⎝ ⎛ − 6 8 0 ⎠ ⎞ × ⎝ ⎛ 0 − m g 0 ⎠ ⎞ + ⎝ ⎛ 1 2 9 0 ⎠ ⎞ × ⎝ ⎛ cos α F C sin α F C 0 ⎠ ⎞ = ⎝ ⎛ 0 0 0 ⎠ ⎞ + ⎝ ⎛ 0 0 6 m g ⎠ ⎞ + ⎝ ⎛ 0 0 ( 1 2 sin α − 9 cos α ) F C ⎠ ⎞ = ( 2 3 cos α − 2 sin α ) F C ( I V ) By comparing equations (III) and (IV) we get ⇒ ⇒ ⇒ 4 3 cos α + sin α 3 sin α tan α α = 2 3 cos α − 2 sin α = 4 3 cos α = cos α sin α = 4 1 = arctan 4 1 ≈ 1 4 ∘ Inserting the result for α in equation (III) or (IV) results F C = 4 3 cos α + sin α m g = 2 3 cos α − 2 sin α m g ≈ 1 . 0 3 ⋅ m g