Balancing a beam
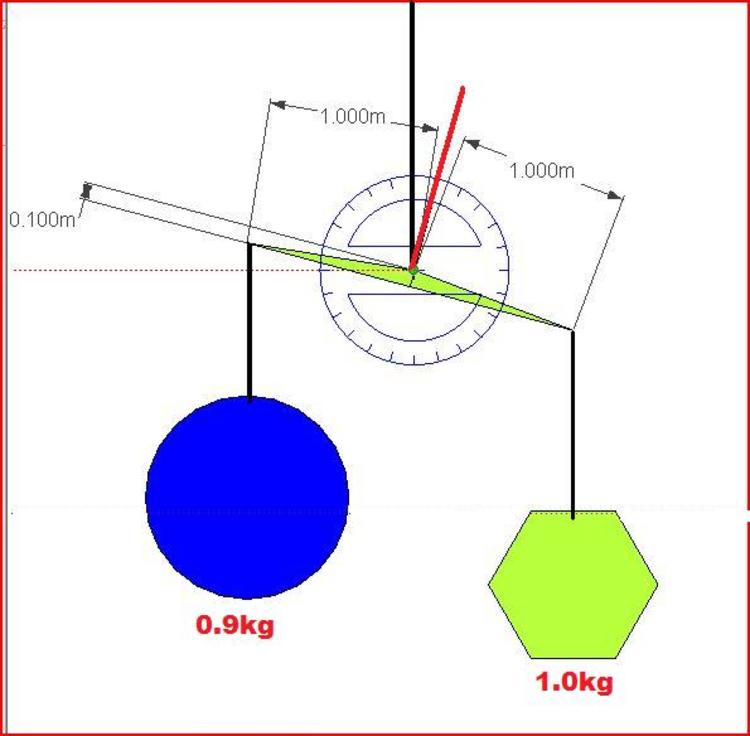 A balance beam is hanging on the black string as shown above. The angle of displacement of the beam from horizontal is indicated on the protractor. What will be the angle read on the protractor with the two weights hanging on the beam as shown?
A balance beam is hanging on the black string as shown above. The angle of displacement of the beam from horizontal is indicated on the protractor. What will be the angle read on the protractor with the two weights hanging on the beam as shown?
Give your answer in degrees.
The answer is 27.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
let A=angle of fulcrum pivot point to end connection point of the weights on beam A = ( c o s ( 0 . 1 / 1 ) = 8 4 . 2 6 0 °
let B= angle of displacement from horizontal of the beam do to hanging weights The beam is rotated clock wise about the fulcrum pivot point by the difference in mass on each end of the beam. The resulting angle from horizontal to the connection point on the left side is increasing A+B and decreeing on the right side A-B.
Sum of moments around center of protractor
0 . 9 ( s i n ( A + B ) ) = 1 ( s i n ( A − B ) ) Using the angle sum and difference identities
0 . 9 ( s i n ( A ) c o s ( B ) + c o s ( A ) s i n ( B ) ) = s i n ( A ) c o s ( B ) − c o s ( A ) s i n ( B ) 0 . 9 s i n ( A ) c o s ( B ) + . 0 9 c o s ( A ) s i n ( B ) = s i n ( A ) c o s ( B ) − c o s ( A ) s i n ( B ) 1 . 9 . c o s ( A ) s i n ( B ) = 0 . 1 s i n ( A ) c o s ( B ) divide both sides by cos(B) cos(A) 1 . 9 s i n ( B ) / c o s ( B ) = 0 . 1 s i n ( A ) / c o s ( A )
Using identity tan(A)= sin(A)/cos(A)
t a n ( B ) = 1 . 9 0 . 1 × t a n ( A ) B = a r c t a n ( 1 . 9 0 . 1 × t a n ( 8 4 . 2 6 0 ) )
B = 2 7 . 6 °