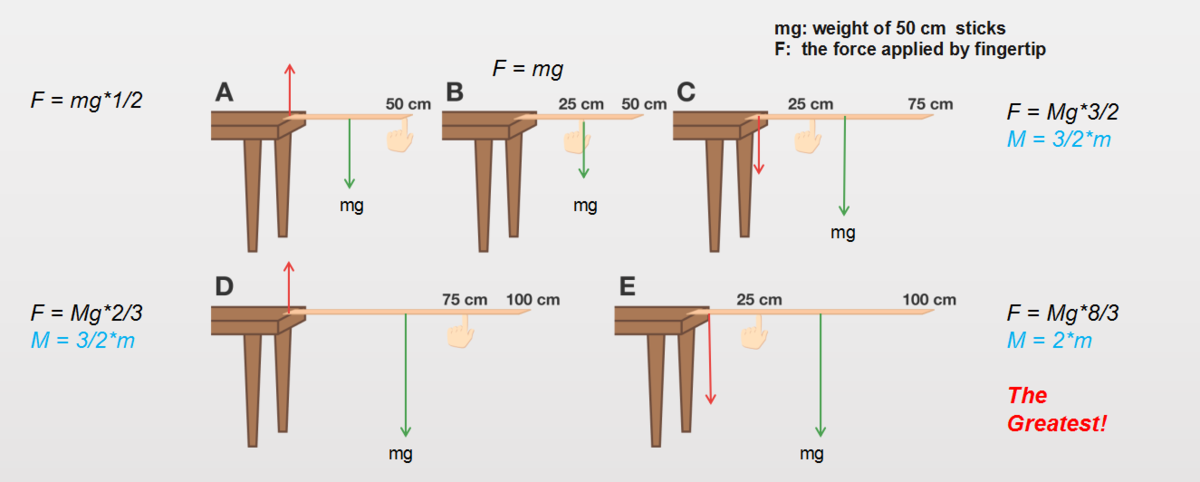
Balancing a rod
Measuring sticks of various lengths are hinged at the edge of a table, with a fingertip supporting the stick somewhere along the stick's length.
When is the force applied by the fingertip the greatest ?
Details and Assumptions :
- All measuring sticks are made of the same material and have the same width and thickness.
- All measuring sticks are divided into 2 5 cm segments.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Ram -- It doesn't appear that you are considering all things involved here; factors additional to distance from the origin are involved. The distance from the finger to the origin is the same in B & C as they are in E -- but there is an additional length of measuring stick involved. A major factor is the center of mass of the stick. This is a classic problem involving the different classes of levers (simple machines).
The point is figure out what direction and size of force to stick applied by the table? let me see three kind of force applied by table. For A,D, force direction is uppward, which applied by table to left side end of stick. The B show size of the force is zero, for C,E show the force is downward, which applied by table to left side end of stick, conclude by Newton's first law, since the sticks at rest, here must be a force pushing upwards from the fingertip to cancel out mg of sticks and force applied by table.
the E is answer, which force applied by fingertips is 8/3 times of the sticks's weight
Shouldn't M D be 2m and not 2 3 × m ? Not that it changes the final result, but i like seeing all the details be correct. ;-)
Log in to reply
Friend, You are right:-) likewise ,I like your coment that make solution perfect, thank you! Owe to good luck,MD is differ greatly with ME,it doest not change result:-)
Consider balancing the moment of the five cases we have:
F l f = m g l c . . . ( 1 )
where
- F --- the force applied by the fingertip
- l f --- the distance between the fingertip and the hinge at the edge of the table
- m --- the mass of the stick
- g --- acceleration due to gravity
- l c --- the distance between the center of mass of the stick and the hinge at the edge of the table
Let the length of the stick be i and the mass per length of the stick be σ . Then l c = 2 l and m = σ l and equation (1) becomes:
F l f = σ l g ⋅ 2 l ⟹ F = σ g ⋅ 2 l f l 2
Since case E has the largest l = 1 0 0 and the smallest l f = 2 5 , F E = 2 0 0 σ g is the greatest .
Chew-Seong -- In the sentence that begins with 'Let the length of the stick...' you have that variable stated as i. However, you then use lower case L as the length in your equation. Is that intentional ? You did not identify lower case L as a variable and you didn't use i in your equations. Please excuse the script here; I haven't learned to use LaTeX yet.
Log in to reply
Sorry, it was a typo. All should be l .
Without any formula it is obvious that F A < F B < F C < F E . Also obvious is F D < F E which leads to E as solution.
Let m be the mass of each identical stick. If a stick is balanced by a force f then as per the law of moments f* distance of the force from the hinge = weight of the stick * distance of center of mass to the hinge. The five cases presented above in the diagram translate to the equations below
CASE A
fx50 = 2m x 25
f = m
CASE B
f*25 = 2m * 25
f= 2m
CASE C
f*25 = 3m * 75/2
f = 4.5m
CASE D
f*75 = 4m * 50
f = 2.67m
CASE E
fx25 =4m * 50
f = 8m
We can see that the highest force has to be applied in case E and the lowest in case A.
Sir, why are you not using latex codes anywhere neither in your questions nor in your solutions.
improve more
The force must make a torque equal to the done by the stick itself. So we look for the stick which makes the largest torque and choose the finger which is closest to the stick's support, which is E .
To apply the greatest force the stick needs to be long and apply the force closer to the table.
Straight to the point awesome!!
Figure E has a long stick with a force applied near the fulcrum/axle. More the force is applied near to the fulcrum, more force it needs to hold the stick.
As E is the longest of all the sticks......
balance the torques acting by forces about the hinge . for first torque about point on table is zero so
f 0.50 = mg 0.25
f=mg/2...
for second similarly
f 0.25=mg 0.25
f=mg
for third
f 0.25=(mg 0.75)/2
f=(mg*3)/2
.....and so on.
Moment of force : M = F × d ⟹ F = d M where, F is the force applied and d is the distance from origin. As all measuring scales are identical they have same moment of force when they are of same length.
From second relation we can come to a conclusion that force applied is inversely proportional to distance from the origin that means lesser the distance from origin more is the force applied. For our convenience let us extend all the scales to 75 cm. The following are the positions of fingertip measured from the table : A : 1 0 0 c m B : 7 5 c m C : 5 0 c m D : 7 5 c m E : 2 5 c m As you can see the least distance is measured in case of E so the greatest force must be applied in case of E and least in case of A.