Balancing forces application

The force of friction between the floor and the plank * $f_{1} = \mu_{2} \times (m_{1} + m_{2}) \times g = 0.5 \times 3 \times 10 = 15 N$ * Now, friction between the plank and the block $f_{1} = \mu_{1} \times m_{2} \times g = 0.2 \times 1 \times 10 = 2 N$ let's first consider the plank the forces $f_{1} and f_{2}$ act on it toward left and * 30 N towards right. so the net force on it is $30 - f_{1} - f_{2} = 30 - 15 - 2 = 13 N$ * so the acceleration of the plank is * F/M = $6.5 m/s^{2}$ . * The only force on the small block is f_{2} = 2 N. Therefore it's acceleration is * F/M = $2 m/s^{2}$ . * the relative acceleration of the *2 * blocks is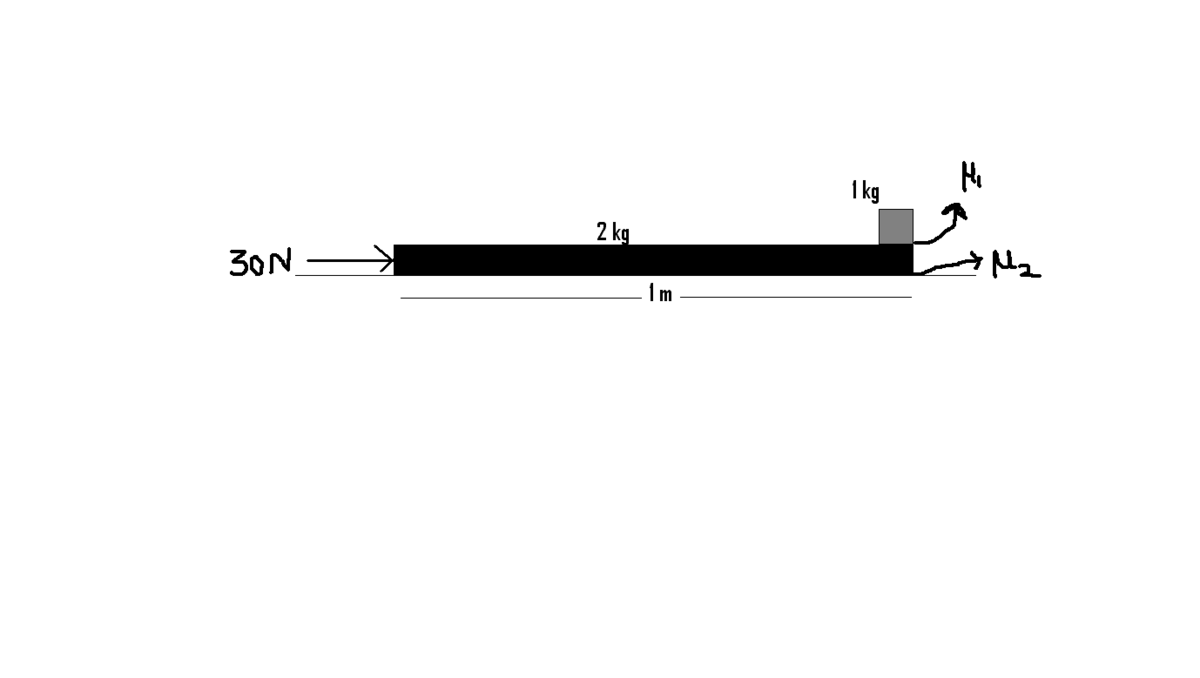

* $6.5 - 2= 4.5 m/s^{2}$ . * now you can use equations of motion to get the time!!!