Balancing Problem - Part 4
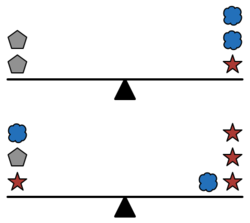 In the above diagram, both beams are balanced.
In the above diagram, both beams are balanced.
How many pentagons would it take to balance 4 clouds?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Gut erklärt!
Let pentagon = p , cloud = c and star = s
Then, 2 p = 2 c + s ........ (1)
& c + p + s = 3 s + c
= > p + s = 3 s
= > s = 2 p
put this value in equation (1)
2 p = 2 c + 2 p
2 c = 2 3 p
Multiply by 2
4 c = 3 p
x=pentagon , y=cloud ,z=star
Now from figure
2x=2y+z --------> (1)
and
x+y+z=y+3z
therefore, x=2z
.Multiplying equation (1) by 2 and substituting x=2z
we get 4y+x=4x
Thus 4y=3x
Thus Four Clouds Equal to 3 Pentagon :D
Great solving by substitution!
let P=1 penta, C=1cloud, S=1star
translate the first and second balance into an eqation; 2P=2C+S (1st balance) S+P+C=C+3S (2nd balance)
combine similar terms in 2nd equation, S+P+C=C+3S P=2S S=P/2 (substitute to the 1st equation)
2P=2C+(P/2) 3P/2=2C 3P=4C
3 Pentagon is needed to balance 4 clouds
Good solution!
We can simply solve it from the condition of the first digram .
weight of 2penta = weight of ( 2cloud + 1 star) this is first condition.
for the the required 4 clouds ,
using condition 1. let 1star = 1cloud .
that is 2penta= 2cloud + 1cloud 2penta= 3clouds
as there are 4 clouds so : adding 1 weight on both sides 1penta + 2penta = 3cloud + 1cloud that is
3penta = 4clouds
hence penta for 4 clouds = 3 Ans.
It is not true that "1 star = 1 cloud".
Since you need 1 star along with 2 clouds to balance the beam with 2 pentagons on the other side, clouds are LIGHTER! So, for 4 clouds you'll need 3 pentagons.
How did you know that it's not 2 pentagons?
1 P = 1 Pentagon
1 C = 1 Cloud
1 S = 1 Star
We can write the following equations:
2 P = 2 C + 1 S
1 C + 1 P + 1 S = 1 C + 3 S
Now, we can rewrite those equations to:
2 P = 2 C + 1 S ⇔ 4 P = 4 C + 2 S
1 C + 1 P + 1 S = 1 C + 3 S ⇔ 1 P + 1 S = 3 S ⇔ 1 P = 2 S
Now, let's put the 2 S = 1 P from the second equation into the first equation:
4 P = 4 C + 2 S ⇔ 4 P = 4 C + 1 P ⇔ 3 P = 4 C
Thus, we need 3 Pentagons to balance 4 Clouds.