Balancing Problem - More Shapes!
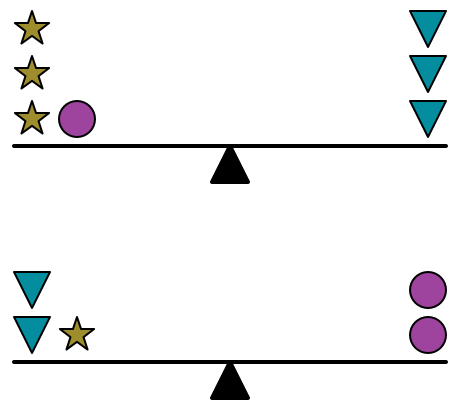 In the diagram to the right, both beams are balanced.
In the diagram to the right, both beams are balanced.
Which of the following options will not balance any of the other options?
Note that there are 5 options (not 4).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Here is another good problem that you may try. https://brilliant.org/problems/who-gets-the-buck-2/ It has been qualified for level 2 algebra but the no. of solvers required is yet not met.
Buddy absolutely wrong...
What question is asked which doesnt balance any of the options all four options are unbalanced and only 4 triangles option is balanced then answer should be
4 triangles
Log in to reply
5 △ = 3 ∘ + 2 ⋆ and 7 ⋆ = 4 △ but 3 △ + 1 ∘ is alone.
Note that there are actually 5 options, and I mentioned that in the question. "4 triangles" would pair up with "7 squares".
Log in to reply
Now I got it what to do....
I was balancing each option so I got that 4 are unbalanced and one is balanced but we have to do it from all 5 options which are balancing or not ....
Thanks for solution and explaination
1 T = 1 Triangle
1 C = 1 Circle
1 S = 1 Star
We can write the following equations:
3 S + 1 C = 3 T
2 T + 1 S = 2 C
First, we can rewrite our first equation from above:
3 S + 1 C = 3 T ⇔ 1 C = 3 T − 3 S
And put it into the second equation:
2 T + 1 S = 2 C ⇔ 2 T + 1 S = 2 ( 3 T − 3 S ) ⇔ 2 T + 1 S = 6 T − 6 S
Rewrite that again to:
2 T + 1 S = 6 T − 6 S ⇔ 2 T + 7 S = 6 T ⇔ 7 S = 4 T
Now, we can cancel the 7 Stars option and the 4 Triangle option from our list, since there is a solution that will balance them. Because the 7 Stars option will be balanced by the 4 Triangle option and the 4 Triangle option will be balanced by the 7 Stars option.
Now, let's see if the 5 Triangles option can be balanced by one of the remaining options. To do so, let's rewrite our first and second equation from the beginning :
3 S + 1 C = 3 T ⇔ 3 S + 1 C + 2 T = 5 T
2 T + 1 S = 2 C ⇔ 2 T = 2 C − 1 S
Now, put the second rewritten equation into the first rewritten equation to get:
3 S + 1 C + 2 T = 5 T ⇔ 3 S + 1 C + ( 2 C − 1 S ) = 5 T
Now, let's rewrite that again to get eventually:
3 S + 1 C + ( 2 C − 1 S ) = 5 T ⇔ 2 S + 3 C = 5 T
And we see that the 5 Triangles option can be balanced by the 2 Stars and 3 Circles option and vice versa. And since we know that one option can't be balanced by any of the other, we know that our remaining option 3 Triangles and 1 Circles must be our desired solution, as we've showed that all other options can be balanced by at least one of the other options.
Hm, I think that trying to figure out which option balances against which becomes tedious. It is not immediately obvious how we should proceed. I feel that it is better to find a solution and then substitute these values in.
Absolutely brilliant
I did the same thing but my final conversions were in fractions of stars
Star(S), Circle(C), Triangle(T)
Given: 3S+C=3T
2C=2T+S
replace C with (2T+S)/2 => 3S + (2T+S)/2 = 3T ----> 7S = 4T (therefore, option 4 and 5 are out)
rewrite option1: 3C + 2S in terms of T ---> (27/7)T + (8/7)T = 5T (option 1 and 2 are out)
remaining option is the 3rd option.
Moderator note:
It helps to express the options in terms of 1 shape, so that we can directly compare them.
Let the masses of circle (round), star and triangle be r , s and t respectively. It is given:
{ 3 s + r = 3 t 2 t + s = 2 r ⇒ 2 t = 2 r − s ⇒ 3 t = r + 3 s ⇒ 6 t = 6 r − 3 s . . . ( 1 ) . . . ( 2 )
⇒ E q . 1 + E q . 2 : E q . 2 : 9 t = 4 r 2 t = 2 r − s ⇒ t = 9 7 r ⇒ s = 2 r − 2 t = 9 4 r
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ Option 1: 5 t Option 2: 3 r + 2 s Option 3: 7 s Option 4: 4 t Option 5: 3 t + r = 5 × 9 7 r = 3 r + 2 × 9 4 r = 7 × 9 4 r = 4 × 9 7 r = 3 × 9 7 r + r = 9 3 5 r = 9 3 5 r = 9 2 8 r = 9 2 8 r = 9 3 0 r
The option that will not balance any of the others is 3 triangles and 1 circle .