Balancing
In figure
A
, the jug on the left pan balances the bottle on the right pan.
In figure
B
, the jug alone balances a mug and a plate.
In figure
C
, three of these plates balance two bottles.
How many mugs will balance a jug?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
You didn't really need to change the third jar to a bottle and back again. Other than that I like this.
Nice solution. For a more general approach to this problem, see Marvin's solution.
effort appreciated!!
1: 2B = 3P (Given Premise C)
2: B = J (Given Premise A)
3: J = 1.5P (1,2)
4: J = P + M (Given Premise B)
5: 1.5P = P + M (3,4)
6: .5P = M (5, 1.5P - P = M)
7: J = 3M (3,6) QED
Thank you! Much easier for me to understand when I see graphics rather than equations.
Best logic to solve the sum. Good work
Very good method, I would never have thought of doing it this way!
let J = jug, B = bottle, M = mug, and P = plate
in figure A ⟹ J = B ( 1 )
in figure B ⟹ J = M + P ( 2 )
in figure C ⟹ 3 P = 2 B ( 3 )
Algebraic solution:
From ( 3 ) , we can say that P = 3 2 B , substituting this in ( 2 ) , we obtain, J = M + 3 2 B . But J = B , so J = M + 3 2 J . Simplifying, we get 3 1 J = M .
Finally, J = 3 M
Very interesting, it seems quite similar to mine.Not to brag but, good job! (That's a logic joke)
This is the logical examination of the problem...the pictorial analysis is but a quixotic search for an answer
nice presentation of solution .. . . .
Much too confusing. From C note three plates equal two bottles. Thus one bottle equals 1.5 plates and that is the half plates. From B we see that one jug equals two half plates and one cup. Therefore, a cup equal one half of a plate. The rest is obvious
Log in to reply
Good. I eliminated the half logic and hope the given solution is understandable even some one is new to algebra. (Add, Replace & Remove logic)
Let J = jug, B = bottle, P = plate, and M = mug.
J = B J = M + P 3 P = 2 B
⟹
3 P = 2 J 3 ( J − M ) = 2 J
⟹ J = 3 M .
Here are the three figures written algebraically... j = b j = m + p 3p = 2b
So you want to find x j = X * m
If we look at figure 2 we see that we have mugs and plates equal to 1 jug. So we have to figure out the weight of mugs and plates relative to a jug.
Start by looking at Figure 3, you have 3 plates equal to 2 bottles. Since jugs and bottles are equal you could also say 3 plates = 2 jugs. Solving for plates we know 1 plate = 2/3 jugs
If we substitute that into Figure 2 we can solve for mugs j = m + 2/3 A mug represents 1/3 of a jug.
Therefore it takes 3 of them to be equal.
Jug = bottle
2(jug) = 2(bottle) and 2(bottle) = 3(plate)
~ thus ~ 2(jug) = 3(plate)
And 2(jug) = 2(mug) + 2(plate)
~ thus ~ 2(mug) + 2(plate) = 3(plate)
So let's say mug is a and plate is b
2a + 2b = 3b
2a = 3b - 2b
2a = 1b
~ therefore ~ 2(mug) = 1(plate)
So 1(mug) + 1(plate) = 1(mug) + 2(mug)
And if 1(jug) = 1(mug) + 1(plate)
Then 1(jug) = 1(mug) + 2(mug)
~ therefore ~ 3 mugs will balance the jug
As you can see in the C balance:
2 bottles=3 plates
So, 1 bottle= 1.5 plates
As per the A balance:
1 bottle= 1 jug
So, 1 jug= 1.5 plates
From balance B:
1 jug= 1 mug+1 plate
So, 1 mug = 0.5 plates
Therefore, 1 jug= 3 mugs
By given figure we have,
J = M + P
3 P = 2 J
First equation gives,
3 J = 3 M + 3 P
= 3 M + 2 J by second equation.
→ J = 3 M
- From A and C: 2 jugs = 3 plates
- Hence 1 jug = 1.5 plates
- From B: 1 jug = 1 plate and 1 cup
Hence from 2 and 3: 1 cup = 0.5 plates 1 jug = 1.5 plates = 3*0.5 plates = 3 cups
Combing A and B, we see that 1 bottle weighs the same as one mug and a plate. Replacing the two bottles on C with 2 mugs and two plates retains the balance on the C scale, So does removing two plates from both sides of C. What's left is one plate on the left and and two mugs on the right. Therefore, one plate weighs the same as two mugs. Returning to B, we then replace the one plate on the right with two mugs, retaining B\s state of equilibrium, proving that one jug weighs the same as three mugs.
Since 1 jug = 1 bottle (A), 2 bottles = 2 jugs, also = 3 plates (C). So 1 jug = 1.5 plates, so 1.5 plates = 1 cup + 1 plate (B). Therefore 1 cup must = .5 plate. So 1jug = 1.5 plates or 3 cups
From A, 1 jug = 1 Bottle
From C, 1 bottle = 1½ plates
Therefore 1 jug = 1½ plates
From B, 1 cup = ½ plate, so that plate can be replaced with 2 more cups to balance, which makes 3.
Quick and easy headcount solution, I'll use j for jug, b for bottle, p for plate and m for mug. From C we get 3p=2b, so if in A 1j=1b, then 2j=2b=3p. From B we get 1j=1m+1p, so 2j=2m+2p, which we previously found out is also 3p. So 2m+2p=3p, so 2m=1p. Since 2j=3p=6m, 1j=3m. Final answer 3 .
1 jug = 1 bottle, 3 plates = 2 bottles, so 3/2 or 1.5 plates = 1 bottle.This means that 1 jug = of a plate, so we can see that 1 jug = 1 plate + 1 mug, so 3/2 of a plate = 1 plate + 1 mug, telling us that 1/2 of a plate = 1 mug, allowing us to easily deduce that 1 jug = 3 mugs.
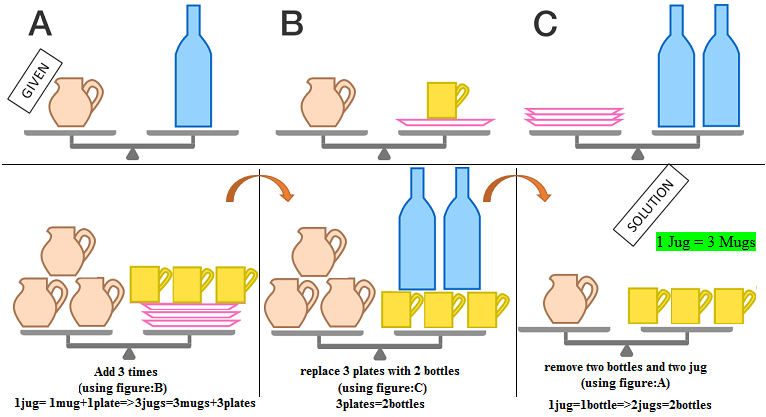
Since one jar balances one mug and one plate (from figure B ), 3 jars balance 3 mugs and 3 plates:
From figure C , replacing the 3 plates with 2 bottles will keep the scale balanced:
From figure A , replacing the 3 jars with 3 bottles will keep the scale balanced:
Now, remove two bottle from both sides, which will keep the scale balanced because we remove the same number of objects from both sides:
Since a jar balances a bottle, per figure A , a jar also balances 3 mugs:
(If you're wondering how I made those pictures, I just took the pic from the problem, cut out the relevant parts, and manipulated them in Microsoft Word.)