Ball Bouncing on Ramp
There is a straight ramp which passes through the origin of the coordinate system and makes an angle of degrees with the positive axis. Gravity is in the negative direction.
A ball is released (starting at rest) from the point . Its first bounce off of the ramp occurs at the origin. How far away from the origin is the ball when it bounces for the third time?
Details and Assumptions: Bounces conserve the kinetic energy of the ball. A bounce multiplies the normal component of the velocity by negative one, and multiplies the tangential component by positive one.
Note:
This was inspired by a question posed by Azimuddin Sheikh. The drawing is not to-scale
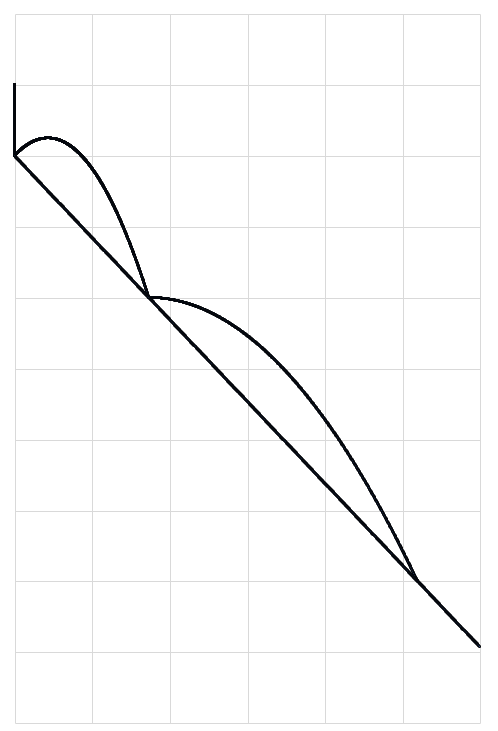
The answer is 12.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Velocity of the ball just before striking the plane for the first time is u=√(20)m/s. Time elapsed between any two consecutive collisions is 2u/g. The distance between first and second collision points is 2u^2/g, and between the second and the third collision points is 4u^2/g. So the total distance is 6u^2/g=6(20)/10=12m.