Ball, Don't Fall! - Part 2
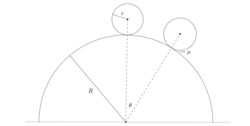 A solid spherical ball of radius
r
=
2
m
is carefully placed on top of a fixed hemisphere of radius
R
=
1
0
m
as shown. It is then pushed very slightly.
A solid spherical ball of radius
r
=
2
m
is carefully placed on top of a fixed hemisphere of radius
R
=
1
0
m
as shown. It is then pushed very slightly.
If the ball doesn't slip till it makes an angle θ = 3 0 o with the vertical, then the minimum required value of coefficient of friction between the ball and the hemisphere is a b − c 2
where a , b and c are co-prime positive integers. Find a + b + c
Details And Assumptions
- Take g = 9 . 8 m s − 2 in the downward direction if needed.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I am now a big fan of yours!👍👍👍👍👍
Did you complete iridov for physics? Are you a repeater (bcs u are18 yrs old) ?
In the first step isn't it mg(R+r)(1-cos30)
In the first step isn't it mgR(1-cos30)
during motion there are two components of acceleration,tangential and radial
mg sin θ - f = ma ...(1)
mg cos θ - N = m ⋅ ( R + r ) v 2 ...(2)
also,by applying torque equation about center of ball
fr= I ⋅ ( r ) a ...(3)
Also,
a= v ⋅ d s d v
where ds= ( R + r ) ⋅ d θ
Therefore,
v ⋅ d v = a ( R + r ) ⋅ d θ ....(4)
from (3) and (1),
f= ( 1 + I m r 2 ) m g sin θ ....(5)
Now,from (3),(4) and (5),
v ⋅ d v = ( I + m r 2 ) m g sin θ ⋅ r 2 ( R + r ) ⋅ d θ
we then integrate this and then substitute v 2 in (2),from this we get N
Then for limiting condition, we use,
f = μ N ....(6)
we substitute the value of N and f in (6) to get coefficient of friction
we then substitute all the values to get the answer.
Using energy conservation between θ = 0 and θ = 3 0 In ICR frame
m g r ( 1 − cos θ ) = 2 1 I b o t t o m ω 2 = 1 0 7 m r 2 ω 2 r ω 2 = 7 1 0 g ( 1 − cos θ ) . . . . . . . ( 1 ) .
Now writing equation in Common normal direction of sphere
m g cos θ − N = m r ω 2 f = μ N = μ g ( m g cos θ − m r ω 2 ) . . . . . ( 2 ) .
Now using torque equation about COM .
τ = f r = 5 2 m r 2 α . . . . . . . ( 3 ) r α = 2 5 μ ( g cos θ − r ω 2 ) . . . . . . ( 4 ) .
Now writing equation along common tangent :
m g sin θ − f = m a c o m . . . . . . ( 5 ) ∵ a c o m = r α . . . . . . . . ( 6 ) .
Now By putting θ = 3 0 . and using all equations we get
μ = 1 7 3 − 2 0 2 .