Ball Fall
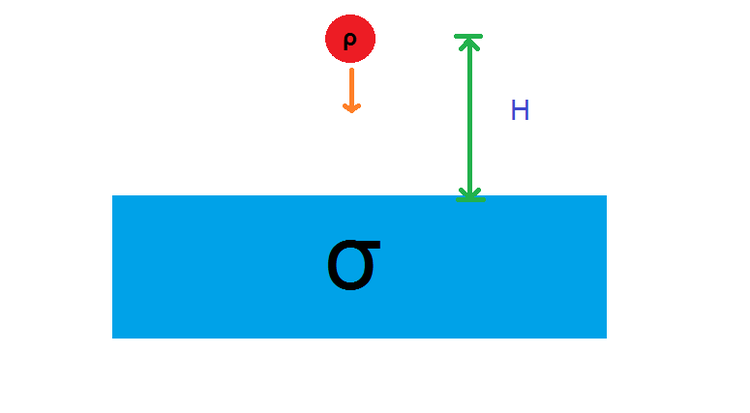 A ball of density
is dropped from rest at a height
into a lake of water with density
such that
. Neglecting damping forces, calculate the maximum depth to which the body sinks before turning around.
A ball of density
is dropped from rest at a height
into a lake of water with density
such that
. Neglecting damping forces, calculate the maximum depth to which the body sinks before turning around.
Assumptions
- , i.e. the ball has some infinitesimal volume .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Net force acting on the ball when it enters the liquid
σ . V . g the buoyant force upwards
And
ρ . V . g the weight of the ball downwards
Here V is the volume of the ball
Let's assume it moves a distance X down in the water.
Applying energy conservation from the point it enters the water to the point it becomes stationary in the water for an instant.
Loss in kinetic energy = Work done against the net force
2 m . v 2 = F . X
2 ρ . V . 2 . g . H = ( σ . V . g − ρ . V . g ) . X
V and g gets cancelled and by rearranging the terms we can find the answer