Ball and Basket

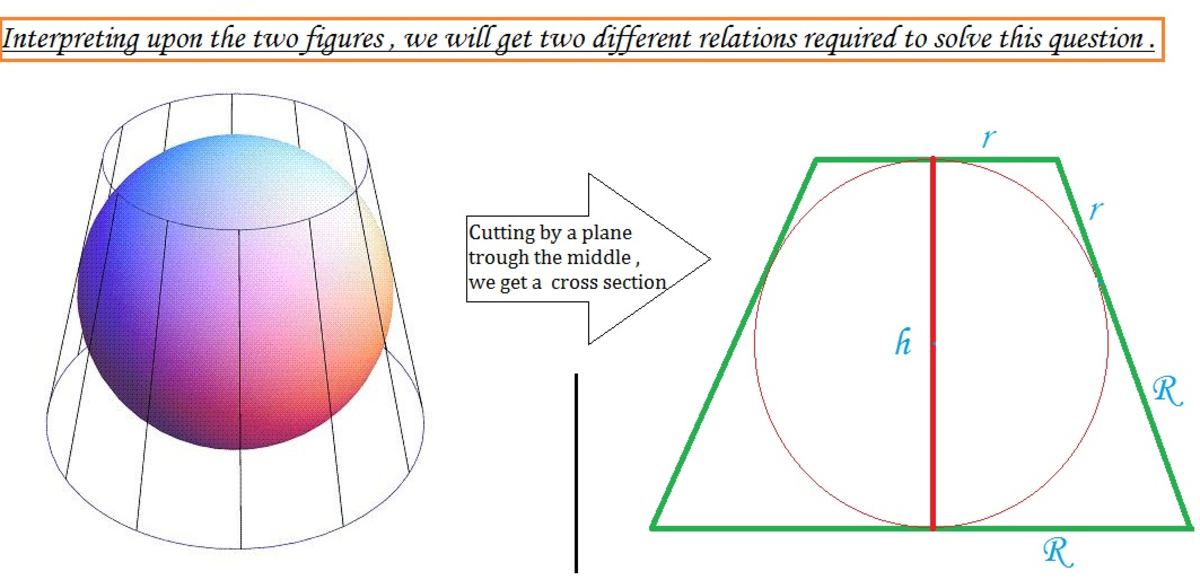
Let $r_1$ be the top radius of the truncated cone, let $r_2$ be the bottom radius of the truncated cone, and let the radius of the sphere be $1.$ Consider the cross section of the figure:

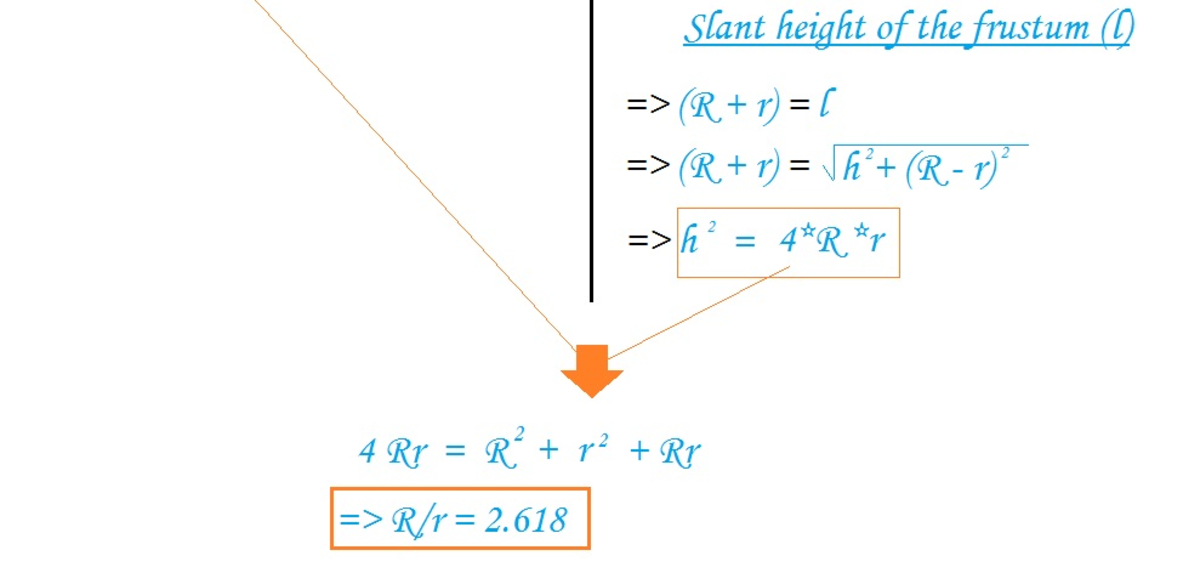
By drawing the radii to the tangents with the cross sectional trapezoid, two kites are formed (they can be proved to be kites using HL triangle congruence). Thus, the slant height of the truncated cone is $r_1+r_2.$

Now consider the right triangle shown below:

By the Pythagorean Theorem,

$\begin{aligned} (r_2-r_1)^2+2^2 &= (r_1+r_2)^2 \\ r_2^2-2r_1r_2+r_1^2+4 &= r_1^2+2r_1r_2+r_2^2 \\ r_1r_2 &= 1 \quad \quad \quad \quad (1) \end{aligned}$

The volume of the sphere and truncated cone are, respectively:

$\begin{aligned} V_S &= \frac{4}{3}\pi r^3 \\ &= \frac{4}{3}\pi \\ \\ V_T &= \frac{1}{3}\pi (r_1^2+r_1 r_2+r_2^2)h \\ &= \frac{2}{3} \pi (r_1^2+r_1 r_2+r_2^2) \end{aligned}$

The volume of the truncated cone is twice the volume of the sphere. Therefore,

$\begin{aligned} \frac{2}{3} \pi (r_1^2+r_1 r_2+r_2^2) &= \frac{8}{3}\pi \\ r_1^2+r_1 r_2+r_2^2 & =4 \quad \quad (2) \end{aligned}$

Recall that $r_1 r_2=1,$ and add this to both sides of the equation to complete the square:

$\begin{aligned} r_1^2+r_1r_2+r_2^2 &= 4 \\ r_1^2+2r_1r_2+r_2^2 &= 5 \\ (r_1+r_2)^2 &= 5 \\ r_1+r_2 &= \sqrt{5} \end{aligned}$

Alternatively, subtract $3r_1r_2=3$ from both sides to complete the square:

$\begin{aligned} r_1^2-2r_1r_2+r_2^2 &= 1 \\ (r_2-r_1)^2 &= 1 \\ r_2-r_1 &= 1 \end{aligned}$

Solving this system of equations gives:

$\begin{aligned} r_1 &= \frac{\sqrt{5}-1}{2} \\ r_2 &= \frac{\sqrt{5}+1}{2} \end{aligned}$

Then the ratio of the larger radius to the smaller radius is:

$\frac{r_2}{r_1}=\frac{\sqrt{5}+1}{\sqrt{5}-1}\approx \boxed{2.618}$

http://artofproblemsolving.com/wiki/index.php?title=2014 AMC 10B Problems/Problem 23. This is the link you find the problem and it's solution. Some how the button for link is missing hence given the full URL.