Ballistic Pendulum Puzzle
A ballistic pendulum, as shown, is a system which can be used to measure the speed of a projectile.
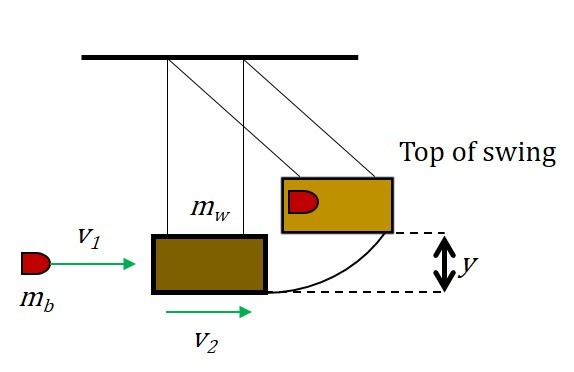
If
(the mass of the bullet),
(the mass of the weight),
and
(the maximum height of block's swing),
find
, the initial velocity of the bullet in meters per second.
Details and Assumptions
- Take as .
- Give your answer to 3 significant figures.
The answer is 355.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Recall that kinetic energy is given by 2 1 × m × v 2 . Therefore, the kinetic energy of the block-bullet unit at the instant after the collision is given by 2 1 × ( m 1 + m 2 ) × v 2 2 .
Also recall that gravitational potential energy is given by m × g × h . The block-bullet unit swings up and comes to rest for an instant at height y , at which point its GPE is thus ( m 1 + m 2 ) × g × y .
Energy conservation gives KE=GPE, yielding 2 1 × ( m 1 + m 2 ) × v 2 2 = ( m 1 + m 2 ) × g × y . Simplifying this yields v 2 = 2 g y .
Now consider the conservation of momentum: m b × v 1 = ( m b + m w ) × v 2 . We can substitute the expression for v 2 which we just found into this momentum equation, yielding v 1 = m b m b + m w × 2 g y .
Now it is simply the case of inputting the given values of m b , m w and y to find the value of the target variable, v 1 :
0 . 0 1 0 . 0 1 + 4 . 0 0 × 2 × 9 . 8 × 0 . 0 4 = 3 5 5 . 0 6 . . . m s − 1
So, to 3 significant figures and without units, the solution is 3 5 5 .