Passing Balls: Hard Version
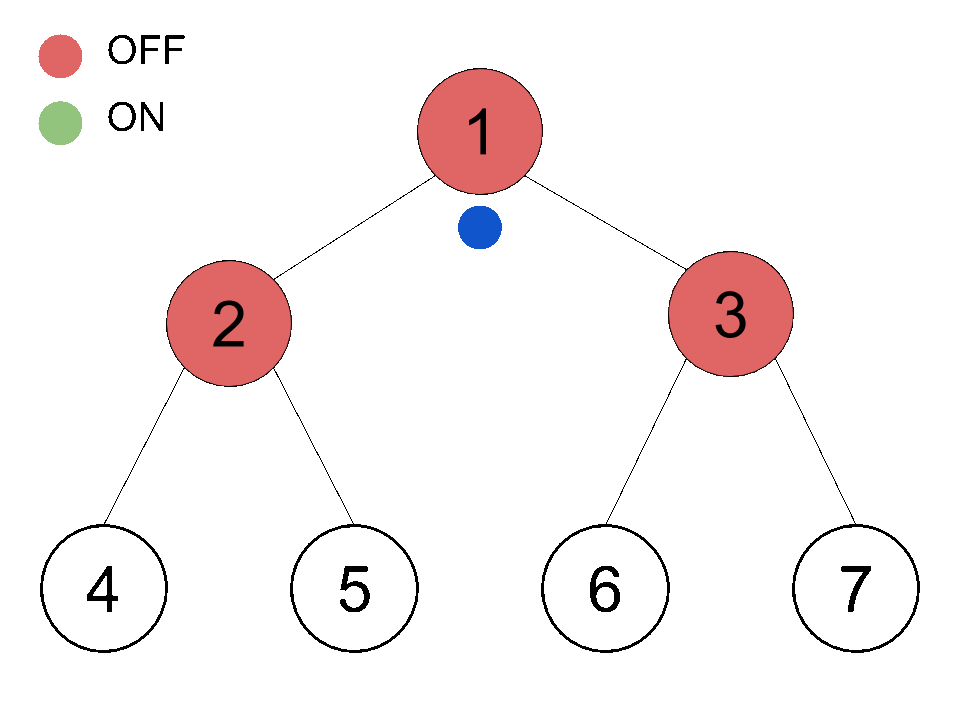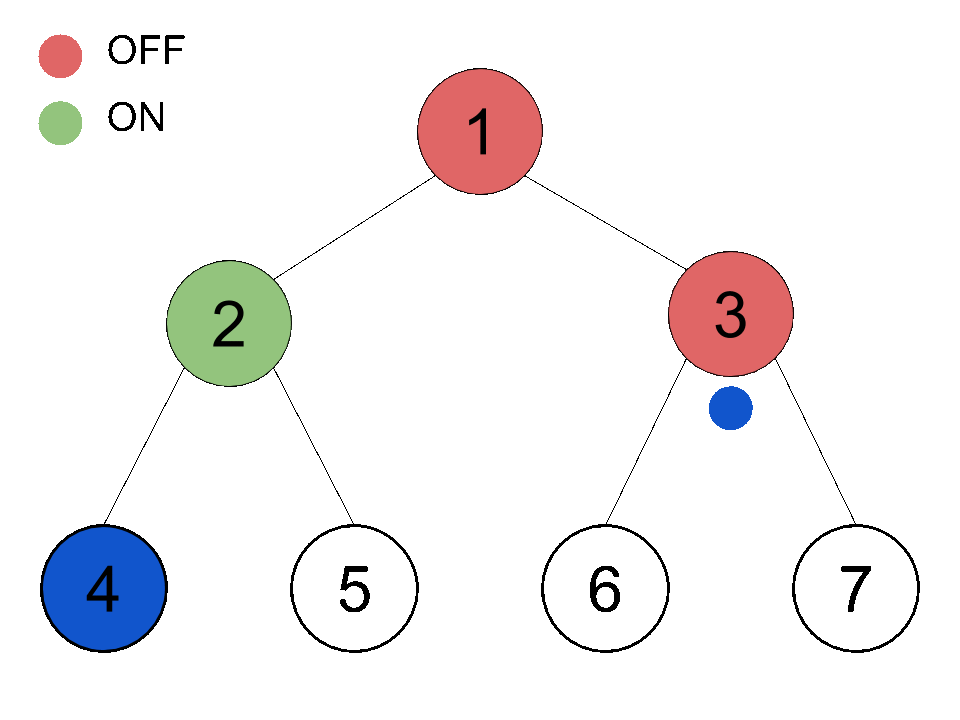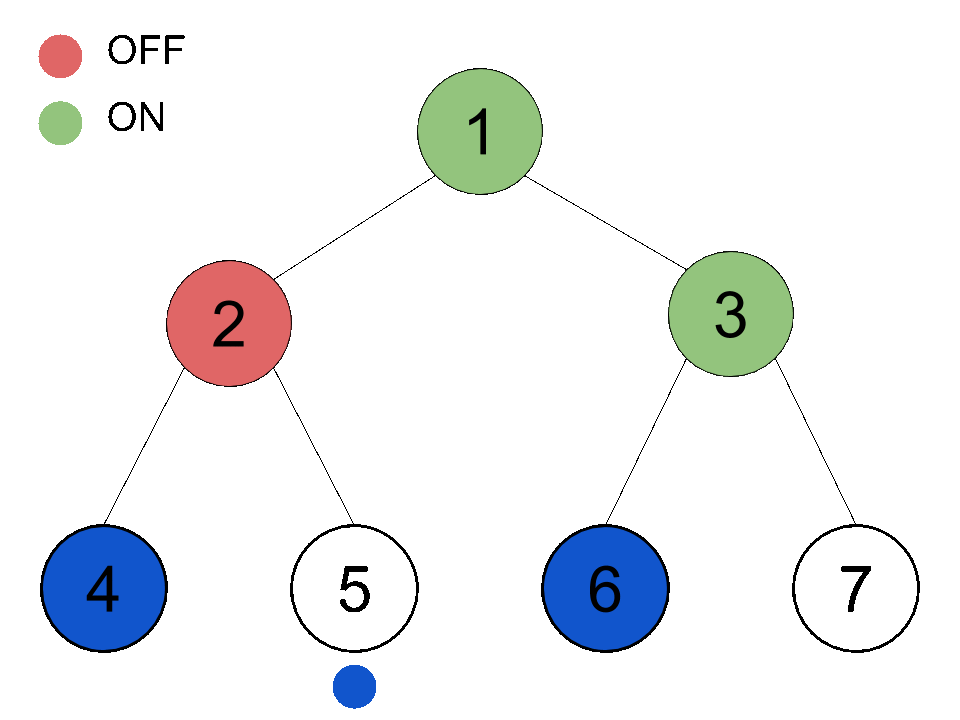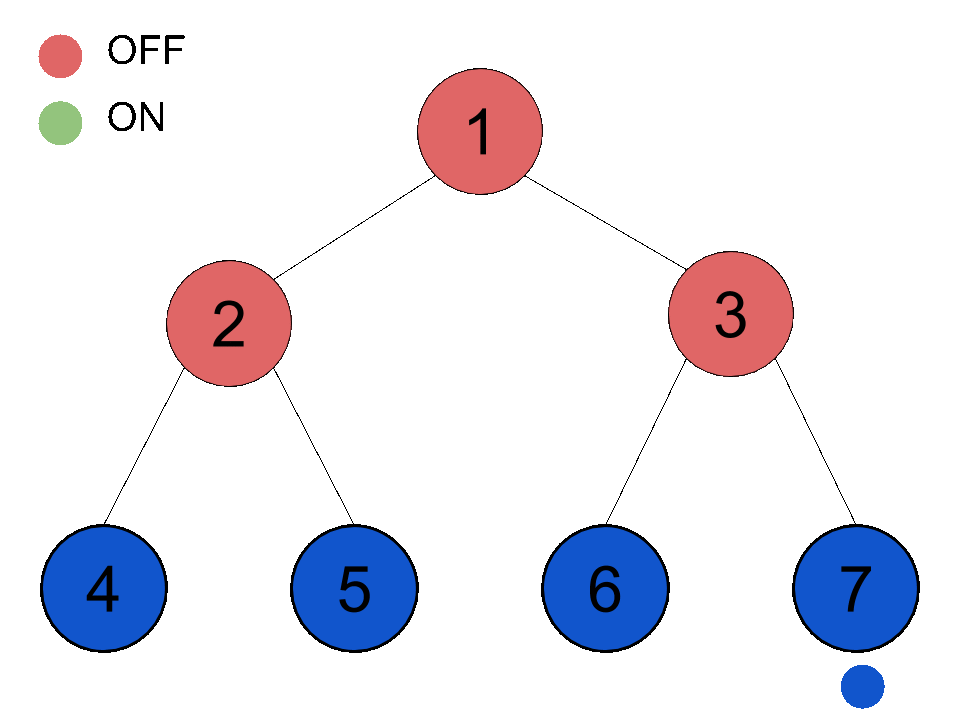
The binary tree above has a height of 2 and has 4 leaves. You are going to pass down a ball from the root (the topmost node). Every node other than the leaves has a switch. If a node is switched off , the ball will pass to its left child; if a node is switched on , the ball will pass to its right child. After passing the ball, the switch will toggle (if it's on it becomes off and vice versa). Initially, every node is switched off.
Chris built a similar tree of height 100 with the same indexing. Which leaf will contain the 3 3 6 6 th ball?
Output you answer modulo 1000.
You are advised to solve the Easy and Medium version of this problem first.
The answer is 936.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Why I get the result 976, not 936, just using your method.
I got my solution from an observation I had. Every ball with even index will be passed to the right child, while every ball with odd index will be passed to the left child. 3366th ball will be passed down to the right child as its 1683rd ball. This 1683rd ball will be passed down to the left child as its 842nd ball. This process repeats recursively, and you can use this to deduce which path the 3366th ball would've took. Once you have the path, it is easy to calculate which leaf the ball would've ended up in. This is my python code which does that.
import math
Ball = 3366
Height = 100
def f(v, ball):
while ball > 1:
v.append(ball % 2 == 0)
ball = math.ceil(ball / 2)
def ff(v):
sm = 1
for dr in v:
sm = sm * 2 + dr
return sm
v = list()
f(v, Ball)
while len(v) < Height:
v.append(False)
print(ff(v))
it outputs 2083143601107473657586501287936. The last 3 digits of this output is 936, which is the answer.
I used a similar method to Laurent, in which I also noticed that the process is related to binary numbers. Why? We can see this recursively: try labeling the nodes of the tree as if they were the leaves of this process for whatever height they are at. We get 1 , 1 , 2 , 1 , 3 , 2 , 4 , 1 , 5 , 3 , 7 , 2 , 6 , 4 , 8 , . . . , and so on.
It is clear to see that each sequence is produced by taking the previous one and inserting k + 2 n after the value k , where n is the height of the tree. Therefore each leaf corresponds to a finite series of distinct powers of 2 . Then it is only natural to pursue the binary expansions.
Furthermore, by our insertion pattern, we see that a one in the binary expansion corresponds to going to the right on the tree. It is a known property of binary trees which are labeled in this way that the left node of a node labeled n is 2 n and that the right node is 2 n + 1 .
Now, since our first node is labeled as 1 , we must look at one less than our desired ball. It is especially handy that we need to read our binary digits backward, and that the binary algorithm works backward. After we run out of binary digits, i.e., we hit the last 1 and go to the right for the last time, we must go left until we are in the last row.
Hopefully, this explanation is very clear; here is my implementation in python, which has variables (height, n) set for generalization:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
This reverse the number 3 3 6 5 1 0 = 0 0 0 ⋯ 0 0 0 1 1 0 1 0 0 1 0 0 1 0 1 2 to 1 0 1 0 0 1 0 0 1 0 1 1 8 8 times 0 0 0 ⋯ 0 0 0 2 = 2 6 3 5 ⋅ 2 8 8 .
Add this to the number of the first leave 2 1 0 0 : 2 6 3 5 ⋅ 2 8 8 + 2 1 0 0 = 2 , 0 8 3 , 1 4 3 , 6 0 1 , 1 0 7 , 4 7 3 , 6 5 7 , 5 8 6 , 5 0 1 , 2 8 7 , 9 3 6
2 6 3 5 ⋅ 2 8 8 + 2 1 0 0 modulo 1000 with a simple calculator:
| powers of 2 | mod 1000 |
| 2 4 | ≡ 1 6 |
| 2 8 | ≡ 2 5 6 |
| 2 1 6 | ≡ 6 5 , 5 3 6 ≡ 5 3 6 |
| 2 3 2 | ≡ 2 8 7 , 2 9 6 ≡ 2 9 6 |
| 2 6 4 | ≡ 8 7 , 6 1 6 ≡ 6 1 6 |
2 8 8 2 1 0 0 = 2 6 4 ⋅ 2 1 6 ⋅ 2 8 = 2 6 4 ⋅ 2 3 2 ⋅ 2 4 ≡ 6 1 6 ⋅ 5 3 6 ⋅ 2 5 6 ≡ 6 1 6 ⋅ 2 9 6 ⋅ 1 6 = 8 4 , 5 2 5 , 0 5 6 = 2 , 9 1 7 , 3 7 6 ≡ 5 6 , ≡ 3 7 6
and answer is 6 3 5 ⋅ 5 6 + 3 7 6 = 3 5 , 9 3 6 ≡ 9 3 6 .
Read the Medium solution first.
Now since the tree is tall and numbers of balls are a lot, we can only pass our algorithm into the computer. Below is the implementation in C++.
Call the function
position(100, 3366)and we will get our desired answer.