Balls in Circles

Logic Level 1

The figure to the right is a peg board used for a game show. Whenever the purple chip falls onto a peg, it has an equal chance to bounce left or right.

If the chip is dropped from the location shown, which position would it most likely fall to?

1 2 3 4 5 6 All of the options are equally likely

9 solutions

Chew-Seong Cheong
Dec 4, 2017

The probability of each peg and the final numbered position is calculated and shown in the figure. It can be seen that position 4 has the highest probability the purple chip would fall to.

Moderator note:

One way to think of the path is as a sequence of "left" and "right" paths. For example, one possible path would be LRLL and another would be RRLL. Since there are a series of 4 binary choices, this means the total number of paths is just $2^4 = 16.$

To land below the starting point, the number of left and right turns needs to be identical. (If we move away from the center, we have to move back an identical amount.) So given 4 turns, choose 2 of them to be moving to the right; this is (4 choose 2).

So the probability of landing in the middle is $\frac{4 \text{ choose } 2}{2^4} .$

By a similar logic we can generalize. Assuming $n$ is the number of steps taken and $n$ is even, the probability of landing right below the starting point is $\frac{n \text{ choose } n/2}{2^n} .$

way undervoted. clear explaination

Oon Han - 3 years, 6 months ago

Thanks. I posted late.

Chew-Seong Cheong - 3 years, 6 months ago

Nice Explanation! Now I can visualize the odds. I solved it in a different way, instead of calculate each probability, I realized that the chip need to bounce in exactly 4 pegs before it reach one of the numbered cups. It give to us $\frac{1}{16}$ probability for each path that the chip would take. Then I find the cup that has the highest number of possible path to reach it. As we can see in your diagram it is the cup number 4 with six possible paths. In fact $6\times \frac{1}{16}=\frac{3}{8}$ .

Victor Paes Plinio - 3 years, 6 months ago

3 and 4 would be equally likely considering the chip falls from the top. The question is misleading.

Orlando Moreno - 3 years, 6 months ago

The question was posed in such a way that assumes possibility of bouncing, not just to fall left or right! So the answer does not square with the question!!! In the question it is said that the chip has an equal chance to $\fbox{bounce}$ left or right! So, what happens if, after bouncing off the peg, the chip hits some upper peg or any other??! Also, there is no information if it a rubber chip, and it is quite legitimate to imply that!

A Former Brilliant Member - 3 years, 6 months ago

I don't really understand how the ball gets to 4 because it could get to 2 as well, I think logical reasoning works best. Why does the ball go to 4 not 2? I would rate this problem a 8 because because I don't really get it. I felt kind of frustrated because there where so many options that where all right.

Lucia Tiberio - 3 years, 6 months ago

The ball won't necessarily go to 4, but the ball have the most probability to get to the cup number 4.

Victor Paes Plinio - 3 years, 6 months ago

Just look for the likelihood and explore all possibilities.

K M - 3 years, 5 months ago

Not that it does not go to 2. It goes to 2 with a probability of 1/16. The problem as for the most likely slot which is 4 with a probability of 3/8.

Chew-Seong Cheong - 3 years, 5 months ago

Kartik Jay
Nov 17, 2017

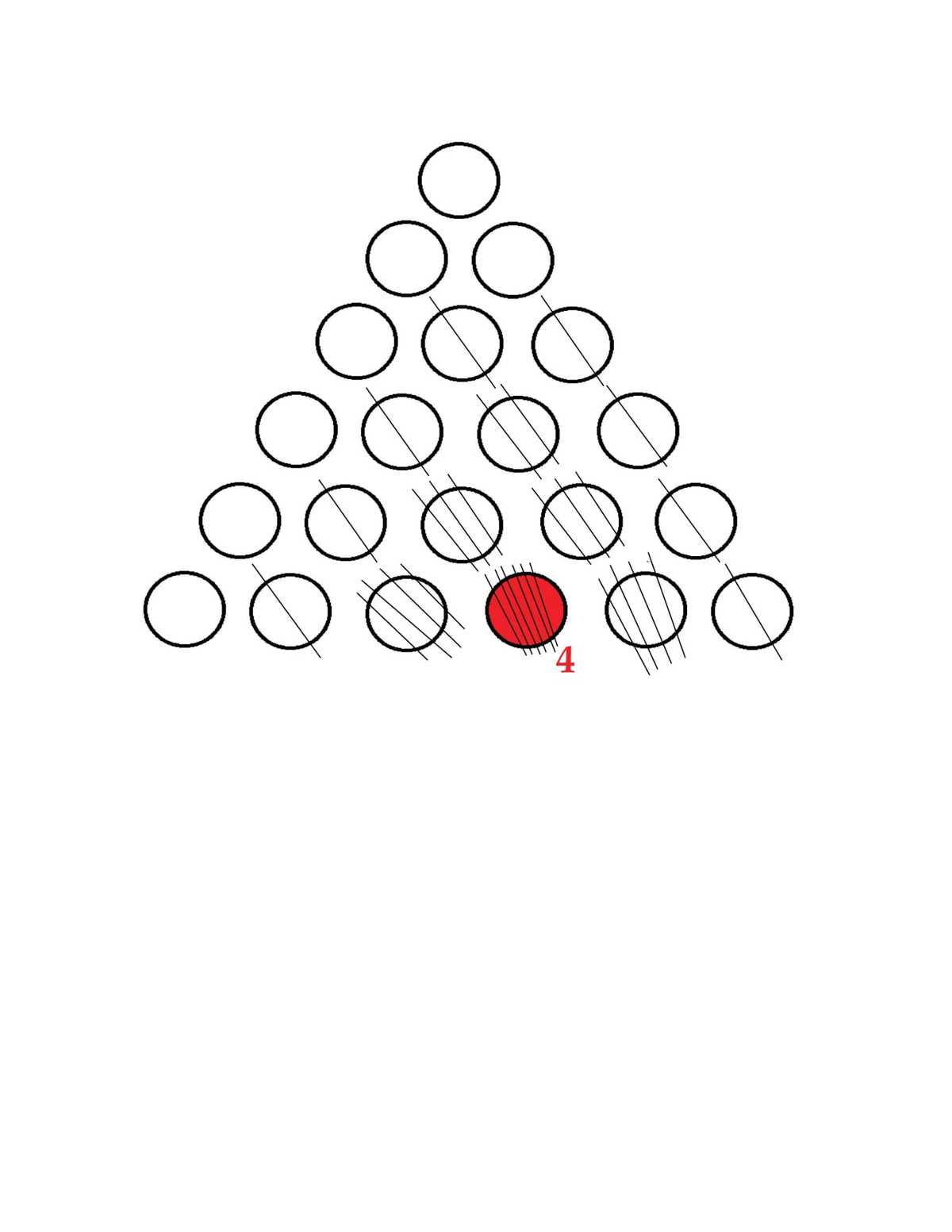A FIGURATIVE SOLUTION TO THIS PROBLEM

This is also Pascal's triangle, with the number in the centre of the row being the largest. This fits in with the combinatorical approach to the problem, as $2 \choose 2$ has the largest value for any of the $n \choose n-4$ combinations of four bounces.

Stephen Mellor - 3 years, 6 months ago

True, it is similar to Pascal's triangle. Nice identification

Syed Hamza Khalid - 3 years, 6 months ago

1 1

1 2 1

1 3 3 1

1 4 6 4 1

Vijay Simha - 3 years, 6 months ago

Ajay Menon
Dec 3, 2017

It's Pascal's triangle

And, what do you mean by that?

Blan Morrison - 3 years, 6 months ago

Pascal’s Triangle can be used when predicting chance on something with even odds (like this example): it’s displayed like a Christmas Tree, with each like you take the sum off the two above, ie:

n=0: 1, n=1: 1 1, n=2: 1 2 1, n=3: 1 3 3 1, n=4: 1 4 6 4 1, n=5: 1 5 10 10 5 1, .... so on... This is commonly used in binomial theorem to find the coefficients when expanding brackets, ie: (a+b)^n

Ex: (a+b)^4 =

(1)a^4 b^0 + (4)a^3 b^1 + (6)a^2 b^2 + (4)a^1 b^3 + (1)a^0 b^4

(Sorry for the above format, hard to express on the iPhone).

As for the problem we can see there are 4 ‘pegs’ the token will encounter therefore n=4 with 6 being the central value / highest probability. We can confirm this visually with the triangle shape the token will fall (the image by Kartic Jay above is a great example). - I may have not explained that above bit how I imagine the problem in my head, anyone is free to correct any of this.

Hope this helps...

Ryan Banks - 3 years, 6 months ago

A Pascal Triangle Is a Special Triangle basically,a triangular array of the binomial coefficients.

Namara Mukhtar - 3 years, 6 months ago

Augusto Schwanz
Dec 10, 2017

I solved this by using pascal's triangle. Imagine pascal's triangle

                1
             1    1
           1   2   1
         1  3  3   1
      1   4  6   4   1
    1  5   10 10  5  1
  1    2   3    4   5   6

The last row is each position that the ball can land on, with the amount of paths it can take on the row above it. However, the ball has already fallen one to the right, so we can redraw pascal's triangle as follows.

                     1
                 0    1
               0   1    1
             0   1    2    1
           0   1   3     3    1
         0   1   4    6    4    1
        1    2   3    4    5    6

Again, the last row is not a part of the triangle, just each position that the ball can land in. ( Note: position 1 has no paths, because after going once to the right it is now impossible to reach that place. ) You can clearly see that position 4 has the most paths that lead to it, so it had the greatest likely hood of be landed in.

Isaque Campello
Dec 8, 2017

It is impossible for the ball to fall in 1, so we discard that option and we also discard the last option, since not all places are equally as likely (the ball can fall anywhere but 1).

The probability for the ball to fall on 2 and 6 are the same, so neither can be the answer. The same logic applies to 3 and 5, since they are symmetrical, so we can discard 3 and 5 as well.

The only option left is 4.

Mads Pihl
Dec 9, 2017

Consider the binomial coefficients when represented in Pascal's Triangle four rows down (the first row is row 0), and observe two properties in the triangle relevant to this problem:

1 - Any given row n (where n is a nonnegative integer) has a total of 2^n choices, so for row 4, as in this case, we have 2^4 = 16 possible outcomes for the final chip position.

2 - Four rows down the combinations are:

4 choose 0 = 1
4 choose 1 = 4
4 choose 2 = 6
4 choose 3 = 4
4 choose 4 = 1.

This gives us the probabilities 1/16, 4/16, 6/16, 4/16, and 1/16 for each combination respectively. And we see from this that 6/16 = 3/8 is the most likely outcome.

Landing on position 4 on the peg board in the problem is the most likely outcome with a probability of 3/8 or .375

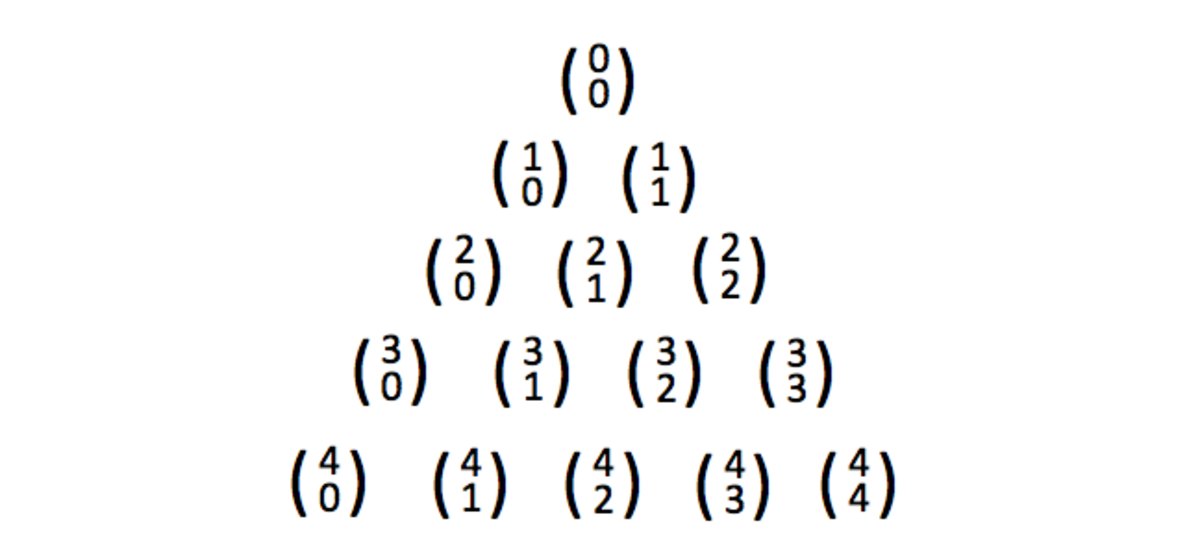
I assumed they would 'bounce' left or right in a horizontal line! And got a different answer.

aeman moges - 3 years, 5 months ago

Janesh G
Dec 9, 2017

Conditions .; Earthly environment like it was on 8 december in the place where i was

It can fall in 2, 3, 4, 5, 6

Now as this type of chain 's middle value is more possible (by logic) Th most oossible slot should be 4 As simple and short as that !! !!

Conditions .; Earthly environment like it was on 8 december in the place where i was

Contact:- [email protected]

Any programers Specialist or any person who know about electronic, electric, robotics, speciality or about music,. Please e mail your special area of intrest and knowledge so it would be useful

[email protected]

K M
Dec 7, 2017

Considering that the chip will fall on to the nearest peg below it after each bounce either left(L) or right(R), the chip will move half unit distance towards or away from a numbered position. Let us consider a single left bounce as (L) and a single right bounce as (R). An L and an R bounced combination will cancel each other, no matter in which level and in which order they occur. Initially, the chip is positioned vertically over 4. An LR bounce combination will result in nothing in the vertical position as the chip will again come vertically over 4. An LL bounce combination will bring the chip over 3. Let us look at the below four letters possible bounce combinations: LLLL -> 2, LLLR -> 3, LLRL -> 3, LLRR -> 4, LRLL -> 3, LRLR -> 4, LRRL -> 4, LRRR -> 5, RLLL -> 3, RLLR -> 4, RLRL -> 4, RLRR -> 5, RRLL -> 4, RRLR -> 5, RRRL -> 5, RRRR ->6. Clearly, the position 4 has maximum occurrence.

Chidiebere Jeffrey
Dec 6, 2017

Its affected mainly by gravity..... So its likely to fall directly downward

That's what the problem is based on. If it doesn't fall downwards then it would not enter any of the spaces, would it?

Saptarshi De Chaudhury - 3 years, 6 months ago

Balls in Circles

9 solutions

Moderator note:

0 pending reports