Balls in Tanks
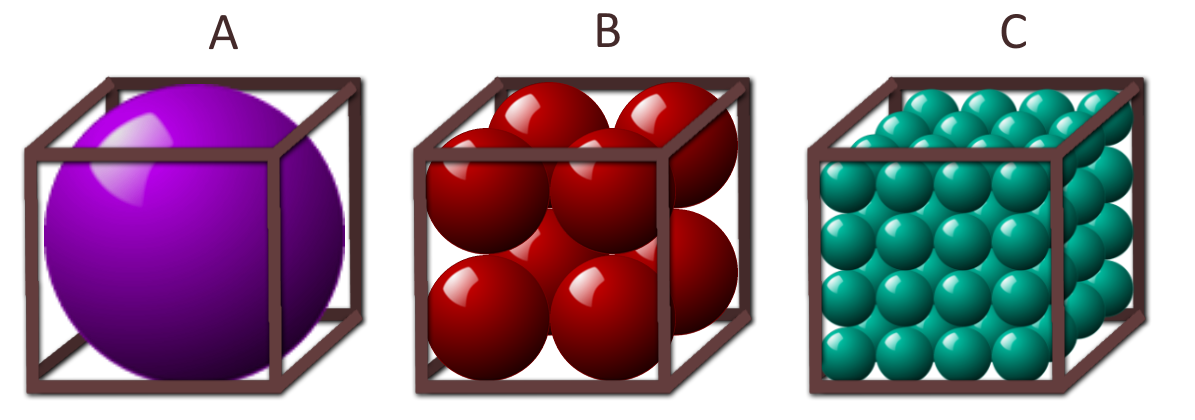 Three identical tanks are shown above. The spheres in a given tank are the same size and packed wall-to-wall. If the tanks are filled to the top with water, then which tank would contain the
most
water?
Three identical tanks are shown above. The spheres in a given tank are the same size and packed wall-to-wall. If the tanks are filled to the top with water, then which tank would contain the
most
water?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Discussions for this problem are now closed
I still didn't got it, Would you please make it a bit low level explaination.
Lets make an assumption. Consider the volume of the tank to be 8 m^3. Now let the empty space in tank be x% of the total volume, in this case x% of 8 m^3. Tank B has 8 balls. Visualize these as 8 balls in 8 identical cubes. Now each of this cube will have empty space x% of total volume, in this case x% of 1 m^3. x% of 8 m^3 = 8 (x% of 1 m^3) Hence Tank A and B have same empty space. Same applies to tank C. I hope this helps.
tnx it really did helped.
Nice! And I think this strategy would even generalize well to much stranger packing problems.
Yeah, I actually got the idea from crystal systems in chemistry. When we calculate the void space or packing fraction or density of a single unit cell of a crystal, we can generalize it to the entire lattice.
Nice connection there
Yes the atomic packing factor helps a lot over here Raj Magesh
If volume of spheres in each cube are same then it is.
good explaination
Great answer!
Thanks...nice method
Analyze what append in a general case where there are m 3 spheres ( m is the number of spheres on an edge of the cube) in a cube with an edge length of l , so find the volume of water filling the gaps around the spheres, which is equal to the difference between the volume of the cube and the volume of spheres. The radius of a sphere is equal to 2 l divided by how many spheres there are on a edge of the cube ( m ).
V w a t e r = V c u b e − m 3 V s p h e r e
V w a t e r = l 3 − m 3 3 4 π ( 2 m l ) 3
V w a t e r = l 3 − m 3 3 4 π 8 m 3 l 3
V w a t e r = l 3 − 6 π l 3
V w a t e r = 6 6 − π l 3
Hence, the volume of water is independent of m and so it's independent of the number of spheres in the cube.
There are thousands of ways to solve the problem. But your solution is the best, as its independent to the number of balls.
Thumbs up for you.
Thank you very much! :)
Whoa whoa whoa!! Wait... I left my physics and maths 3 years ago... Can you make it little easy?! And tell me.,. How do you know that volume 4 cubes in BB= Volume of 9 cubes inc=volume of that cube?!?
I'll clear some points:
1) The volume of the sphere is V s p h e r e = 3 4 π r 3 , where r is the radius. The radius of a sphere is equal to l divided by how many spheres there are on a edge of the cube (so we get the diameter), divided by 2 (radius = diameter/2). Hence V s p h e r e = 3 4 π ( 2 m l ) 3
2) m is the number of spheres on an edge of the cube, and so m 2 is the number of spheres on a face of the cube (square) and m 3 is the number of spheres in the cube. For example in the tank B there are 2 spheres on an edge, 4 on a face, 8 in the cube; in the tank C there are 4 spheres on an edge, 16 on a face, 64 in the cube; in the tank A there are 1 sphere on an edge, 1 on a face, 1 in the cube.
3) Doing some calculus, as showed above, m is cut out and we get that V w a t e r = 6 6 − π l 3 , so the volume of water is independent of m . The volume of water depend only on the length of the edge of the cube, but we know that are three identical tanks, so they have the same edge length and so the same volume of water.
I hope to have cleared all your doubts.
You have a very clear explanation that answered all my query to the problem. Thank you!
Simplify problem.
In the first tank (1 ball), if R=4 then (psuedo) V = 4^3=64
The second tank(8 balls) r=2 then V= (8)(2^3) = 64.
the last tank(64 balls) r=1 then V=(64)(1^3) = 64.
There for, the same volume.
Another take on this: the volume of a sphere grows with the cube of its radius. (r^3). If the sphere in cube A has radius r, then the spheres in cube B, have radius r/2 and volume diminished (r/2)^3 (ignoring the constant 4pi/3 here). However we have 8 spheres so the total volume grows, 8*(r/2)^3 which is r, same as the one big sphere.
The ratio sphere/free water will always be the same.
Whatever the calculation, the ratio at some point is going to be 1 : 1/8 ∗ 8 : 1/64 ∗ 64
Lets take the volume of the cube be V m^3 (same in all cases) First case: Sphere radius : r Sphere volume 4 π r^3 = S (say) Empty space = V-S m^3 Second case: Sphere radius : r/2 Sphere volume : 4 π (r/2)^3 No. of spheres : 8 Total volume of all the spheres : 4 π r^3 = S Thus empty space is again same. Again for the third case, radius of each sphere is r/4 No. of spheres are 64, so the volume of all the spheres is again S. Thus the empty space will be the same for all the three cases and hence the amount of water that can be filled too will be the same. So to generalise, as long as the spheres are perfectly packed and fill the tank face to face, how many the balls may be (of course of equal size) , empty space will be the same.(Can be proved using simple mathematics).
Radius of the first sphere is a/2, Volume of the first sphere is 4/3 22/7 (a/2)^3. Radius of each sphere in the second tank is a/4, volume of all spheres together is (4/3 22/7(a/4)^3) 8. Both volumes are equal. Similarly for spheres in third tank. Since volumes of three tanks are the same and spheres occupy equal volume in each tank, the remaining volume of water is the same too.
This is very simple to solve just by looking at it, you really have to think about it. I'm 13 and I got it correct and when it said only 38% got it correct.... Wow... I'm not saying your stupid but its an easy question.
It seems to me that your solutions are all too complex.
Assume that the cube is 4 units. That means the water displaced by A would be 1 6 π = π × r 2 .
Then cube B would be 2 2 × 4 (since they're one-fourth the size of A) or also 1 6 π .
Finally cube C would be 1 2 × 1 6 × π or again 1 6 π .
Since volume of cubes is same, the water displaced is the same
They itself said it has same size that is they cover equal volume
simply size of the cubes are same and the volume of the cubes sholuld be same so they occupy same amount of water
Let's start with the single sphere.
If you halve the radius of this sphere, you will end up with a smaller sphere that is 1/8 of the volume of the original (since the volume of a sphere is given by 4/3 times pi times radius cubed).
However, you can fit 8 of these smaller spheres inside the tank so the total volume of "sphere-material" remains unchanged.
The same applies when you halve the radius of this smaller sphere and so on and so forth.
To generalize, the volume of an individual sphere decreases at exactly the same rate as increase in the number of these spheres that fit inside the tank.
The solutions below make this too complicated.... The additional info reads the spheres within a given tank are all the same size and are packed to fit wall to wall. This sentence lets you assume no matter what, the volume occupied by the sphere is always the same. The tanks are identical therefore each scenario has the same amount of water....
This is the second time a question seemed like common-sense to me, and I thought no equation was necessary, but I still see people in the comment feed using some crazy-looking mathematics. Am I doing it wrong?
It says "three identical tanks". So therefore they're the same size and will hold the same amount of water. Its simple, no need for extensive amounts of equations.
Let r be the radius of the smallest sphere. There are 64 in all. There vol is 64x4/3 X pie r3. Radius of red sq is 2r. There are 8 sheres..vol is 8X4/3 X pie (2r)3 . similarly vol of purple sh is 4/3 x Pie (4r)3. all the vols are same . So vol of cube - vol of spheres is the same...
They all contain the same amount of water because the total volume of the balls will remain the same as 1 ball is getting divided into 4 balls and then 64 balls So the total volume of the box - the total volume of the balls will remain the same in all 3 boxes
1 ball is getting divided into 8 balls.
Common sense: if all spheres are equal size then if amount of liquid is the same in all tanks
They are identical boxes, in other words they are all the same. Therefore, they will all hold the same amount of water. Doesn't take a math genius to figure that out.
When it was said that the units are all the same then common sense stated the water is the same on all units.
An intuitive solution: