Balls in the vase
Logic
Level
2
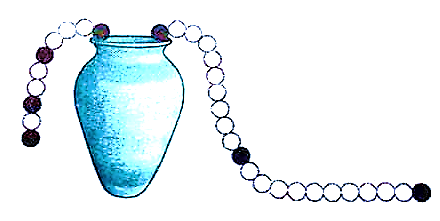
In the vase shown above, a necklace of black and white beads is inserted. The number of white balls between each consecutive black ball follows an arithmetic progression.
How many balls in total does the necklace have?
34
55
66
You can not know
32
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
If we understand the problem of counting the balls inside and outside, we have to:
White balls are: 1 + 2 + 3 + . . . + 9 + 1 0 = 2 1 0 ( 1 0 + 1 ) = 5 5
(The Gaussian formula was used)
Black balls are a total of 1 1 .
Total balls are:
5 5 + 1 1 = 6 6