Passing Balls: Medium Version

Computer Science Level 4

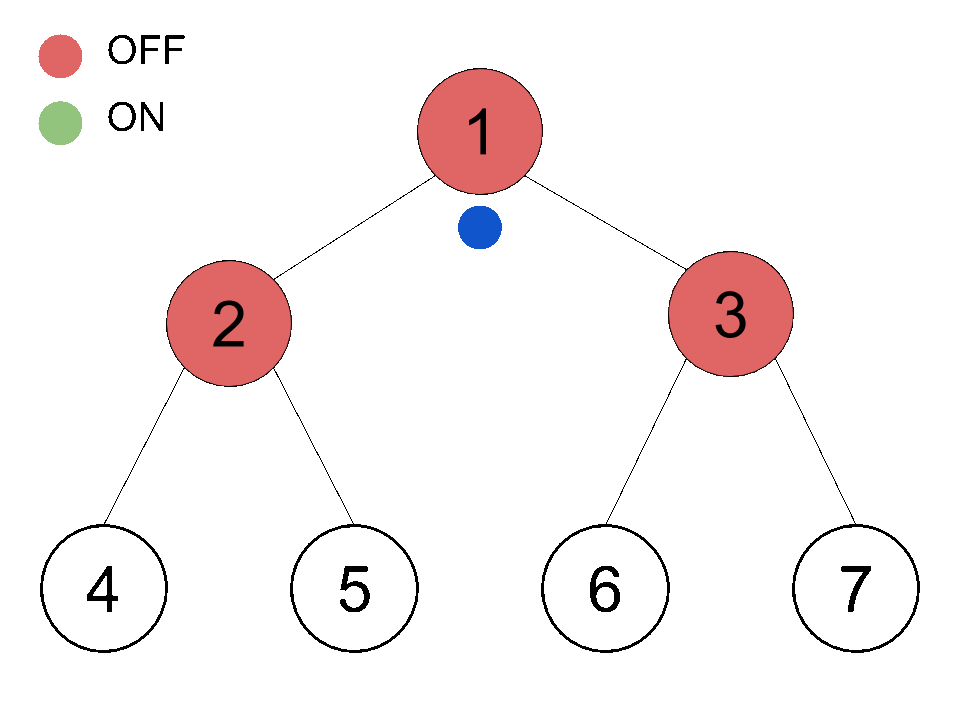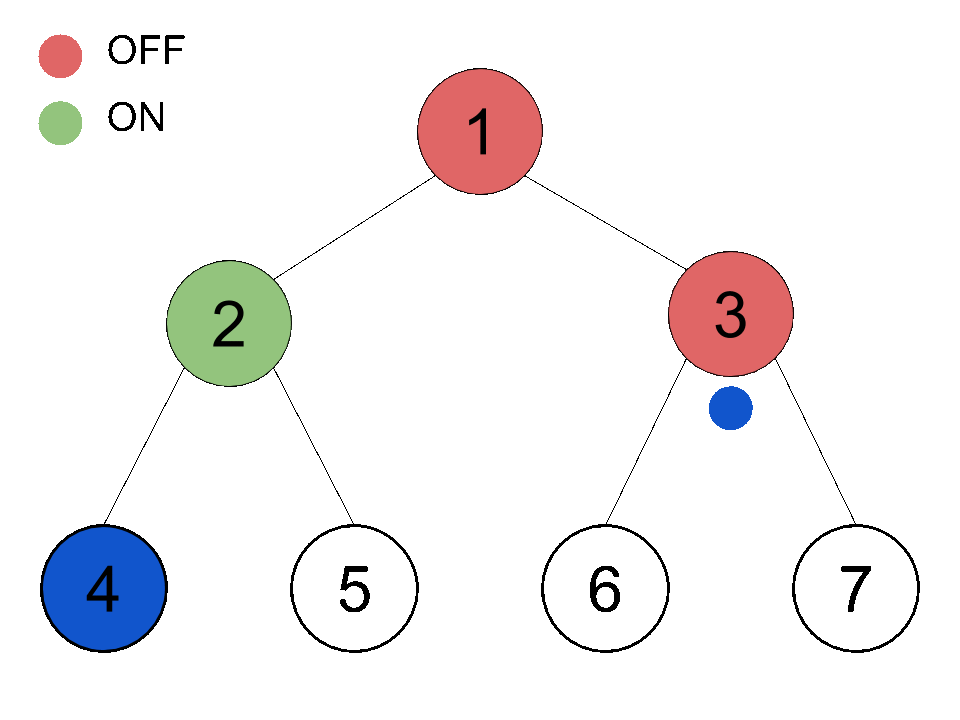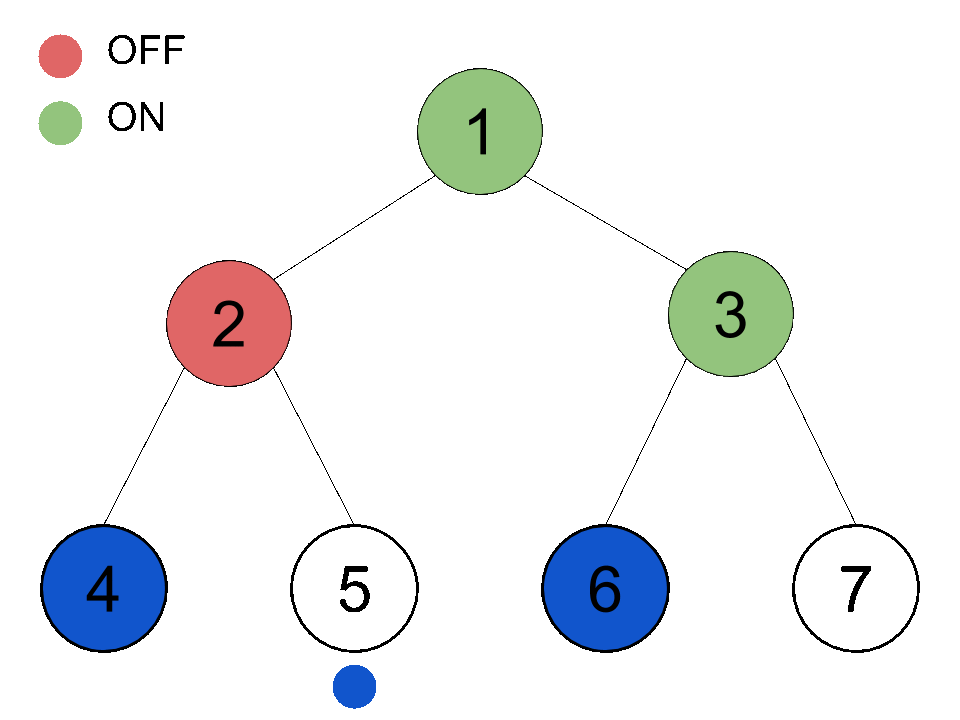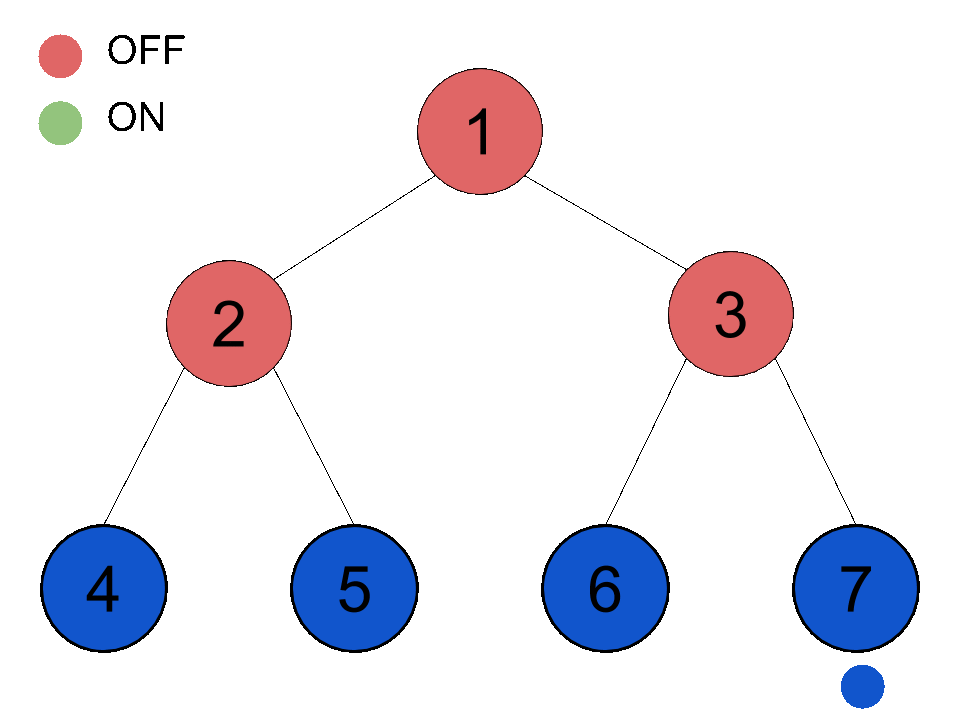
The binary tree above has a height of 2 and has 4 leaves. You are going to pass down a ball from the root (the topmost node). Every node other than the leaves has a switch. If a node is switched off , the ball will pass to its left child; if a node is switched on , the ball will pass to its right child. After passing the ball, the switch will toggle (if it's on it becomes off and vice versa). Initially, every node is switched off.

Chris built a similar tree of height $8$ with the same indexing. Which leaf will contain the $36^\text{th}$ ball?

Note : the indexes of the leaves should be in the range $[256,512)$ .

You are advised to solve the Easy version of this problem first.

Find this too simple? Try the Hard version of this problem.

The answer is 452.

2 solutions

Christopher Boo
May 15, 2016

By some observation, we can find a pattern. The algorithm is as follow :

x is the index of the node that contains the ball.

    x = 1
    p = 36;
    do height = 8 times :
        if p is odd
            x = (2 * x)
            p = (p + 1) / 2
        if p is even
            x = (2 * x + 1)
            p = p / 2

With this algorithm, we can still compute the final position of the ball by hand.

height	x	p
0	1	36
1	3	18
2	7	9
3	14	5
4	28	3
5	56	2
6	113	1
7	226	1
8	452	1

The desired answer is $452$ .

Laurent Shorts
Feb 20, 2017

This algorithm reverse the bits of the number in base 2, with input: the balls numbered from 0; output: leaf 256+result.

The $36^\text{th}$ ball is numbered $35_{10}=00100011_2$ . Reverse the digits to get $11000100_2=196$ , so the ball ends on the leaf number $256+196=\boxed{452}$

Passing Balls: Medium Version

You are advised to solve the Easy version of this problem first.

Find this too simple? Try the Hard version of this problem.

The answer is 452.

2 solutions

0 pending reports