Balti Physics!!
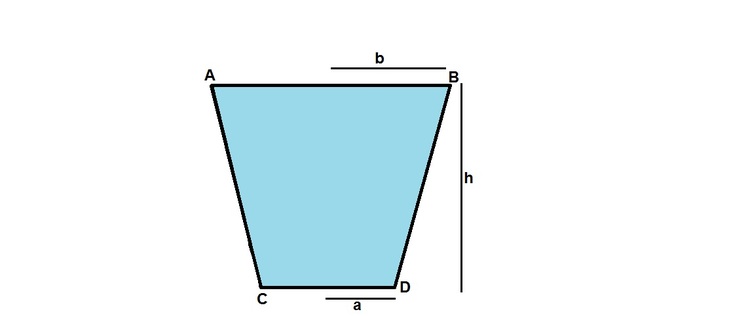 A bucket ( also known as "Balti" in Hindi ! ) is fully filled with water. The bucket has the shape of a symmetrical frustum of upper radius "b" and lower radius "a". It is of height "h". Find the net downward force (in SI Units) that the water exerts on the sides of the bucket i.e, sides AC and BD. Neglect atmospheric pressure.
A bucket ( also known as "Balti" in Hindi ! ) is fully filled with water. The bucket has the shape of a symmetrical frustum of upper radius "b" and lower radius "a". It is of height "h". Find the net downward force (in SI Units) that the water exerts on the sides of the bucket i.e, sides AC and BD. Neglect atmospheric pressure.
NOTE -
a= 0.5 m
b= 1 m
h = π 3 m
g = 1 0 m / s 2
Density of water = 1 0 3 k g / m 3
The answer is 10000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 figure
Downward force acting on an elemental strip as shown is equal to
ρ
∗
g
∗
y
∗
2
∗
π
∗
x
∗
cos
θ
d
y
∗
sin
θ
.
⇒
total downward force on the sides of the bucket is equal to
∫
0
h
ρ
∗
g
∗
y
∗
2
∗
π
(
b
−
y
∗
tan
θ
)
∗
tan
θ
∗
d
y
=
ρ
∗
g
∗
2
∗
π
∗
tan
θ
∗
∫
0
h
(
b
−
y
tan
θ
)
∗
y
∗
d
y
=
ρ
∗
g
∗
∗
2
∗
π
∗
tan
θ
[
2
b
∗
h
2
−
tan
θ
∗
3
h
3
]
.
Now,
tan
θ
=
h
b
−
a
=
6
π
,
x
=
(
b
−
y
∗
tan
θ
.
)
Substituting values,we getnet downward force on the sides of the bucket
=
1
0
,
0
0
0
N
.
Solution by my Dad not by me!
figure
Downward force acting on an elemental strip as shown is equal to
ρ
∗
g
∗
y
∗
2
∗
π
∗
x
∗
cos
θ
d
y
∗
sin
θ
.
⇒
total downward force on the sides of the bucket is equal to
∫
0
h
ρ
∗
g
∗
y
∗
2
∗
π
(
b
−
y
∗
tan
θ
)
∗
tan
θ
∗
d
y
=
ρ
∗
g
∗
2
∗
π
∗
tan
θ
∗
∫
0
h
(
b
−
y
tan
θ
)
∗
y
∗
d
y
=
ρ
∗
g
∗
∗
2
∗
π
∗
tan
θ
[
2
b
∗
h
2
−
tan
θ
∗
3
h
3
]
.
Now,
tan
θ
=
h
b
−
a
=
6
π
,
x
=
(
b
−
y
∗
tan
θ
.
)
Substituting values,we getnet downward force on the sides of the bucket
=
1
0
,
0
0
0
N
.
Solution by my Dad not by me!
Your dad is simply BRILLIANT!
The volume of a conical frustum is given by:
V f = 1 / 3 × h × π × ( r 1 2 + r 1 × r 2 + r 2 2 )
For our case substituting a and b for r 1 and r 2 we get a total volume of:
1 . 7 5 m 3
The lower horizontal surface holds the weight of the water placed exacly above it. The rest of the water is hold by the sides. We need to determine the volume of the water which is N O T above the lower horizontal surface(the circular disk with radius a )
The volume of the water above the lower horizontal surface is the volume of a cylinder with radius a and height h .
So we have V c y l = π × a 2 × h = 0 . 7 5 m 3
Taking the difference we get:
V s i d e = V f − V c y l = 1 m 3
but the water density is 1 0 3 k g / m 3
So M a s s s i d e = 1 0 3 × 1 = 1 0 3 k g
W e i g h t = M a s s × g = 1 0 4 N = 1 0 , 0 0 0 N
Yes correct solution. Based on the concept of hydrostatic paradox.