Bamboo Forest
You are surveying a rectangular area of a bamboo forest of square feet. The four bamboos at the corners are each feet high, and when you analyze the surface area at the top, you find that it is a partial plain of as shown below.
Assuming the area is densely packed with bamboos, what is the average height of these bamboos in feet?
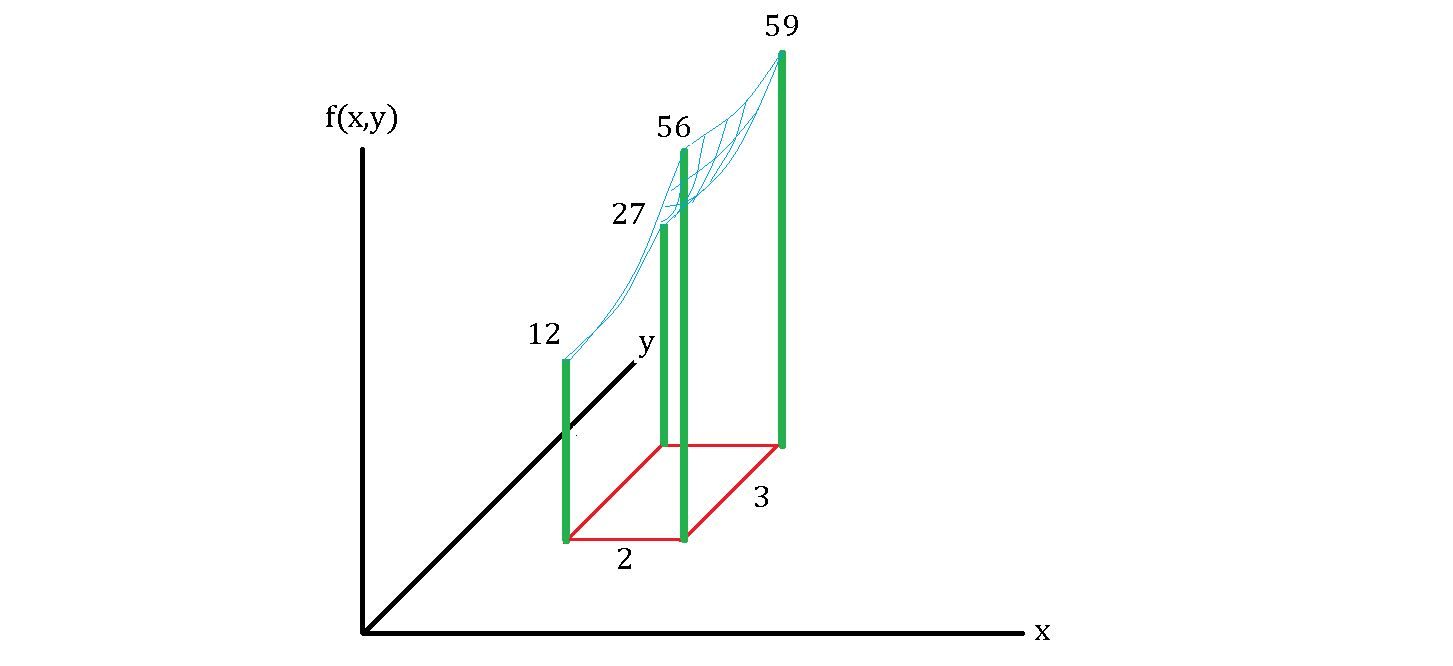
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose the point nearest to the origin is ( a , b ) . Then f ( a , b ) = b 2 + a 3 − 2 a b + 7 = 1 2 and f ( a , b + 3 ) = ( b + 3 ) 2 + a 3 − 2 a ( b + 3 ) + 7 = 2 7
f ( a , b + 3 ) − f ( a , b ) = 1 5 = 6 b + 9 − 6 a ; b = a + 1 .
f ( a , b ) = ( a + 1 ) 2 + a 3 − 2 a ( a + 1 ) + 7 = 1 2
a 3 − a 2 − 4 = 0
( a − 2 ) ( a 2 + a + 2 ) = 0
Thus, a = 2 and b = 3 .
Now we can set up a region of [ 2 , 4 ] × [ 3 , 6 ] for f ( x , y ) , and the average height of the bamboo can be calculated as the ratio total volume over the base area. The volume in this case = ∫ 2 4 ∫ 3 6 y 2 + x 3 − 2 x y + 7 d y d x
Taking the first integral, ∫ 3 6 y 2 + x 3 − 2 x y + 7 d y = [ 3 y 3 + y x 3 − x y 2 + 7 y ∣ ∣ ∣ ∣ 3 6 ] = 3 x 3 − 2 7 x + 8 4
Then taking the second integral, ∫ 2 4 3 x 3 − 2 7 x + 8 4 d x = [ 4 3 x 4 − 2 2 7 x 2 + 8 4 x ∣ ∣ ∣ ∣ 2 4 ] = 1 6 8 + 1 8 0 − 1 6 2 = 1 8 6 .
Therefore, the average height = 2 × 3 1 8 6 = 3 1 .