Bandpass filter
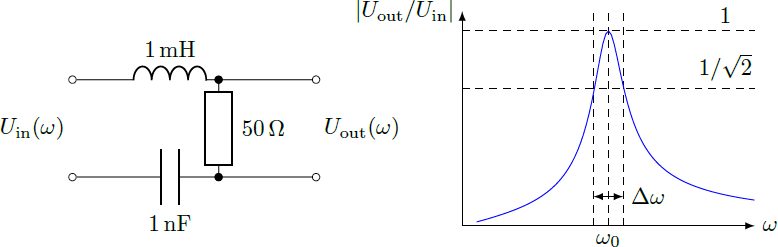
An electrical resonant circuit consisting of an inductance , a resistance and a capacitance can be used as a bandpass filter. From the input signal , only frequencies near the resonance are then forwarded as output signal . For a sinusoidal signal , an output voltage is then obtained with a frequency-dependent amplitude , which has a maximum at the resonance frequency . This peak is characterized by its full half-width at which the electrical power has fallen to half the maximum value (or ). The relative bandwidth can be expressed by the dimensionless Q factor What is the Q factor for the resonant circuit shown here?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The resonant circuit has an complex electrical impedance Z = I U in = i ω L + R + i ω C 1 = R + i ω L ( 1 − ω 2 ω 0 2 ) The voltage drop at the resistor is taken as output signal ⇒ ⇒ U out A ( ω ) ∣ A ( ω ) ∣ = R I = Z R U in = U in U out = 1 + i ω R L ( 1 − ω 2 ω 0 2 ) 1 = 1 + ω 2 R 2 L 2 ( 1 − ω 2 ω 0 2 ) 2 1 To estimate the bandwidth Δ ω , we put ∣ A ( ω ) ∣ = 1 / 2 , so that ⇒ ⇒ ⇒ ⇒ ω R L ( 1 − ω 2 ω 0 2 ) ω 2 ± L R ω − ω 0 2 ω 1 , 2 Δ ω Q = ± 1 = 0 = ± 2 L R + 4 L 2 R 2 + ω 0 2 = ω 1 − ω 2 = L R = Δ ω ω 0 = R 1 C L = 2 0