Bang the box
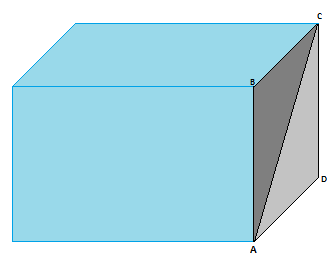
There is a cuboidal box which is filled with liquid of density . Let & be the force applied by the liquid on and , respectively.
Find .
Bonus: Solve this problem without using calculus.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There is a property that the total force on an area inside any fluid is equal to the pressure applied by that fluid at the center of the area × total area
now let a r e a o f Δ A B C = a r e a Δ A D C = Δ
and when we calculate the depth of the center of both the triangle we will sea that the depth of the center of Δ A D C is twice the depth of the center of Δ A B C
so F 2 F 1 = δ × g × 2 h × Δ δ × g × h × Δ = 0 . 5
where δ = d e n s i t y g i v e n l i q u i d
h = d e p t h o f c e n t e r o f Δ A B C
g = a c c e l e r a t i o n d u e t o g r a v i t y