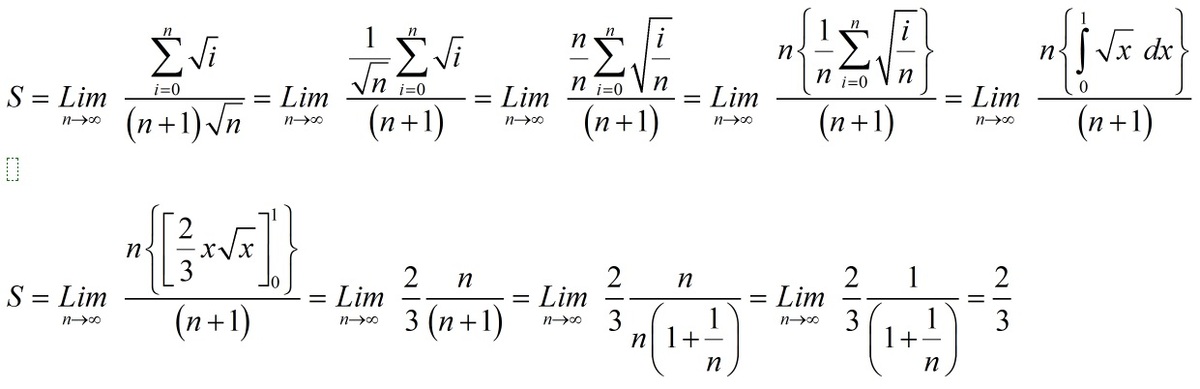Barrows Sum
n → ∞ lim ( n + 1 ) n i = 0 ∑ n i
Suppose the limit above equals to b a where a , b are coprime positive integers, find a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note that ∫ 1 n x − 1 d x ≤ i = 0 ∑ n i ≤ ∫ 0 n x d x . Then, we can solve both integrals and divide each member of the above inequalities by ( n + 1 ) n , leading us to 3 2 ( n + 1 ) n ( n − 1 ) 3 / 2 ≤ ( n + 1 ) n i = 0 ∑ n i ≤ 3 2 ( n + 1 ) n n 3 / 2 . We know that when n → ∞ , the lower and upper bounds tend to 3 2 . This allow us to conclude, by the Squeeze theorem , that ( n + 1 ) n i = 0 ∑ n i = 3 2 .