Basic geometry problem
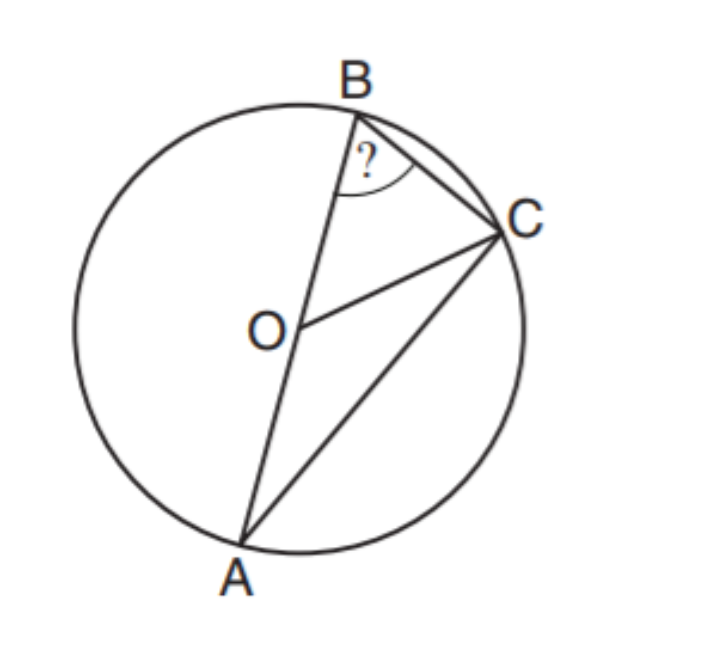
∠ B O C = 5 0 ∘ ,
The triangle A B C is enclosed within the circle, the center of the circle is O
∠ C B O = ?
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
BOC and COA are supplementary angles,meaning that their sum is 180 degrees.From there we obtain COA =130 degrees.We next use our definition of a circle to determine that the triangle COA is isosceles,meaning that the remaining angles of COA must be equal.Using algebra(COA+2x=180,130+2x=180,2x=50,x=25),we find that OCA and OAC(we need OCA)are both 25 degrees.By visual intuition we find that OCA and BCO are complementary,meaning BCO=90-OCA=90-25=65.Finally,by the sum of the angles of a triangle we find that CBO=180-(BOC+BCO)=180-(50+65)=180-115=65DEGREES.
By the Inscribed Angle Theorem, ∠ B A C has half of the amplitude of the angle ∠ B O C which means that ∠ B A C = 2 5 o .
By Thale's Theorem when we have a triangle inscribed in a circumference and one of its sides is a diameter of the circumference, the opposite angle will be a right triangle. So, the triangle A B C is a right triangle. Then ∠ C B O + ∠ B A C + 9 0 = 1 8 0 .
Solving the above equation we find that ∠ C B O = 6 5 o .
Note that OB = OC = radius of the circle. So triangle BOC is an isosceles triangle. So angle OBC = angle OCB = (180 - 50)/2 = 65 degrees.
Since triangle BOC has one vertex on the center of the circle and the other two vertices are on the circle, two sides of the triangle are also radii of the circle. This makes the sides congruent, so triangle BOC is isosceles.
In an isosceles triangle, the angles opposite the congruent sides are congruent. Since angle BOC is given to be 50 degrees and the sum of the triangle's angles must add up to 180 degrees, each base angle must have a measure of 65 degrees.