One Train After Another
Classical Mechanics
Level
3
The graph above shows the position of two trains over time which run on parallel tracks. For time , which of the following is true?
At time
, both trains have the same velocity
Somewhere on the graph, the acceleration of both trains is the same
The speed of both trains is constantly increasing
At some time before
, both trains have the same velocity
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
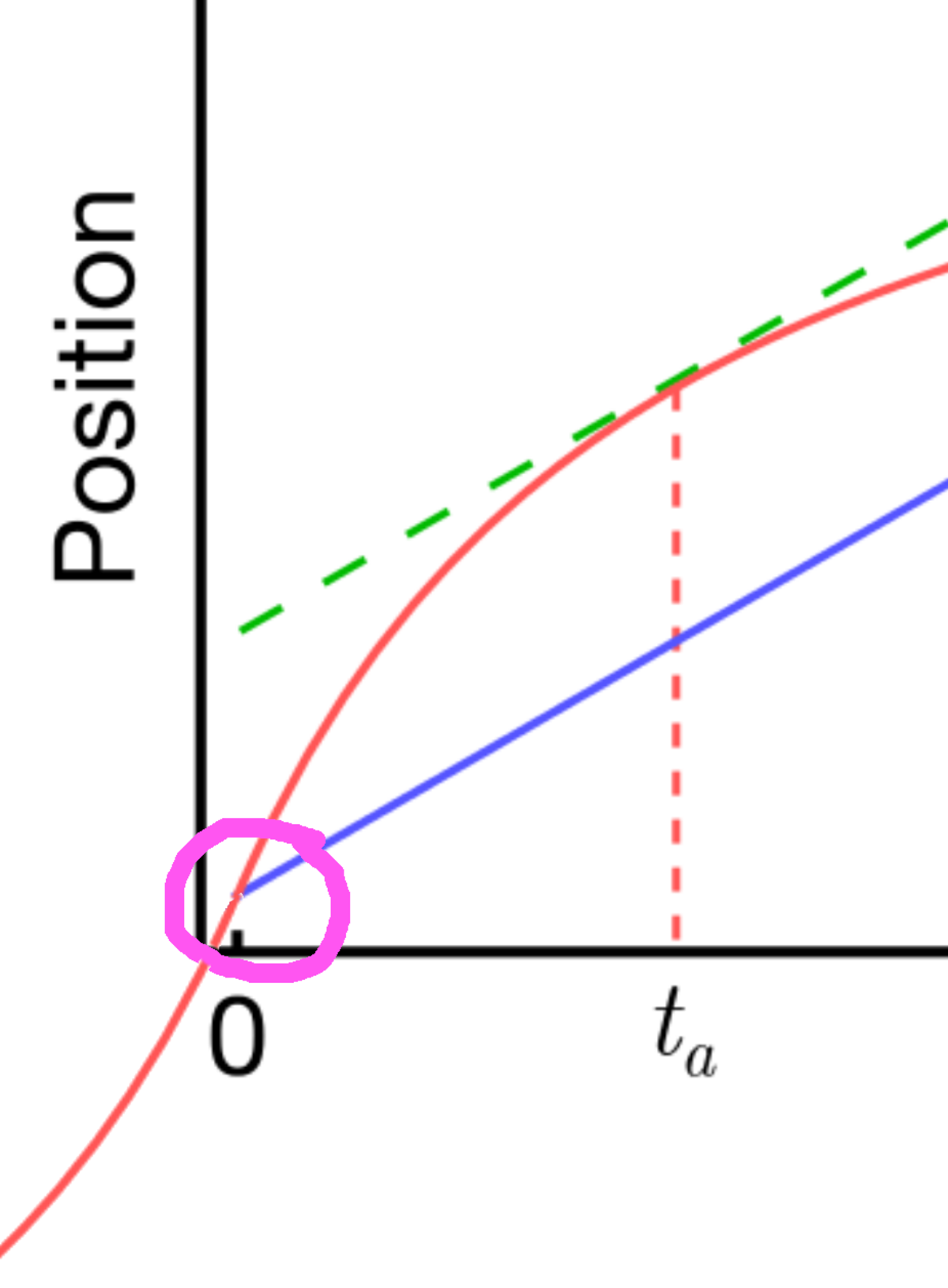
The gradient of a point on the above graph gives the velocity of the train at that instant.
The gradient of train 2 is constant so its speed is constant, and the slope of train 1 is approaching zero, so its speed is approaching zero. Hence, "The speed of both trains is constantly increasing" is incorrect.
The gradient of train 2 is constant, so its velocity is constant and its acceleration is zero. The gradient of the red curve decreases continuously, so its acceleration is never zero. Hence, "Somewhere on the graph, the acceleration of both trains is the same" is incorrect.
Since the gradients of the red curve and blue line are different at t b , the velocities of the trains is not same at t b .
By the mean value theorem , there exists t a < t b , such that the velocity of train 1 has the same value as the velocity of train 2.