Basic question at geometery
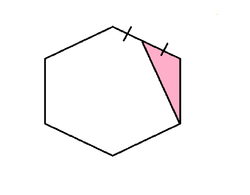 Find the area of the shaded region if the area of the regular hexagon is 24.
Find the area of the shaded region if the area of the regular hexagon is 24.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
divide the hexagon to three parallelogram and then divide one of the parallelogram in two equal part and then the resultant part to half.so
intially area is divided to 24/3 =8 and each parallelogram divided to half of area so 8/2 =4 and then that sectional area to half you will get 4/2 =2 that the result of the given ques
Just assume that the hexagon is regular (because there is nothing that says anything to the contrary) and divide the hexagon into 6 equilateral triangles, each with an area of 4. Since the shaded triangle shares the base with one of the triangles and has one half its height the area thus becomes 2.
Area of the hexagon = 6*( sqrt(3)/4) a^2 = 24, which gives a^2 = 16/sqrt(3).
Area of the shaded region = (1/2)* a* (a/2)* sin(60) = (sqrt(3)/8) a^2 = (sqrt(3)/8) (16/sqrt(3)) = 2
The pink area is half the area of one of the six identical triangles the hexagon can be divided into. Since each triangle is one-sixth the area of the hexagon, the pink area is 2 1 × 6 1 = 2 × 6 1 = 1 2 1 the area of the hexagon, which is 1 2 2 4 = 2
Using the area A of the hexagon (24), find the length of the sides using the formula:
s
=
3
1
/
4
×
s
q
r
t
2
A
/
9
=
3
1
/
4
×
s
q
r
t
2
(
2
4
)
/
9
=
3
.
0
3
9
3
4
Then, find the apothem of the hexagon (note: the apothem is the distance the center to the midpoint of side) using the formula:
a
p
o
t
h
e
m
=
s
/
(
2
t
a
n
×
1
8
0
/
n
)
where n is the number of sides of the polygon so,
a
p
o
t
h
e
m
=
3
.
0
3
9
3
4
/
(
2
t
a
n
×
1
8
0
/
6
)
=
2
.
6
4
After that, multiply the side to the apothem (this is to determine half area (a) of the rhombus that will be produce by connecting 2 midpoints to 2 corners of the hexagon).
a
=
3
.
0
3
9
3
4
×
2
.
6
4
=
8
.
0
2
4
Then subtract the a to half of A.
1
2
−
8
.
0
2
4
=
3
.
9
8
Then divide it by 2 to get the answer
3
.
9
8
/
2
=
1
.
9
9
o
r
2
Assuming that the hexagon is regular, its area can be divided into 6 identical equilateral triangles, each of area 6 2 4 = 4 .
The shaded triangular area shares a base with one of these equilateral triangles and has one-half its height. Thus it will have one-half its area, i.e., 2 4 = 2 .