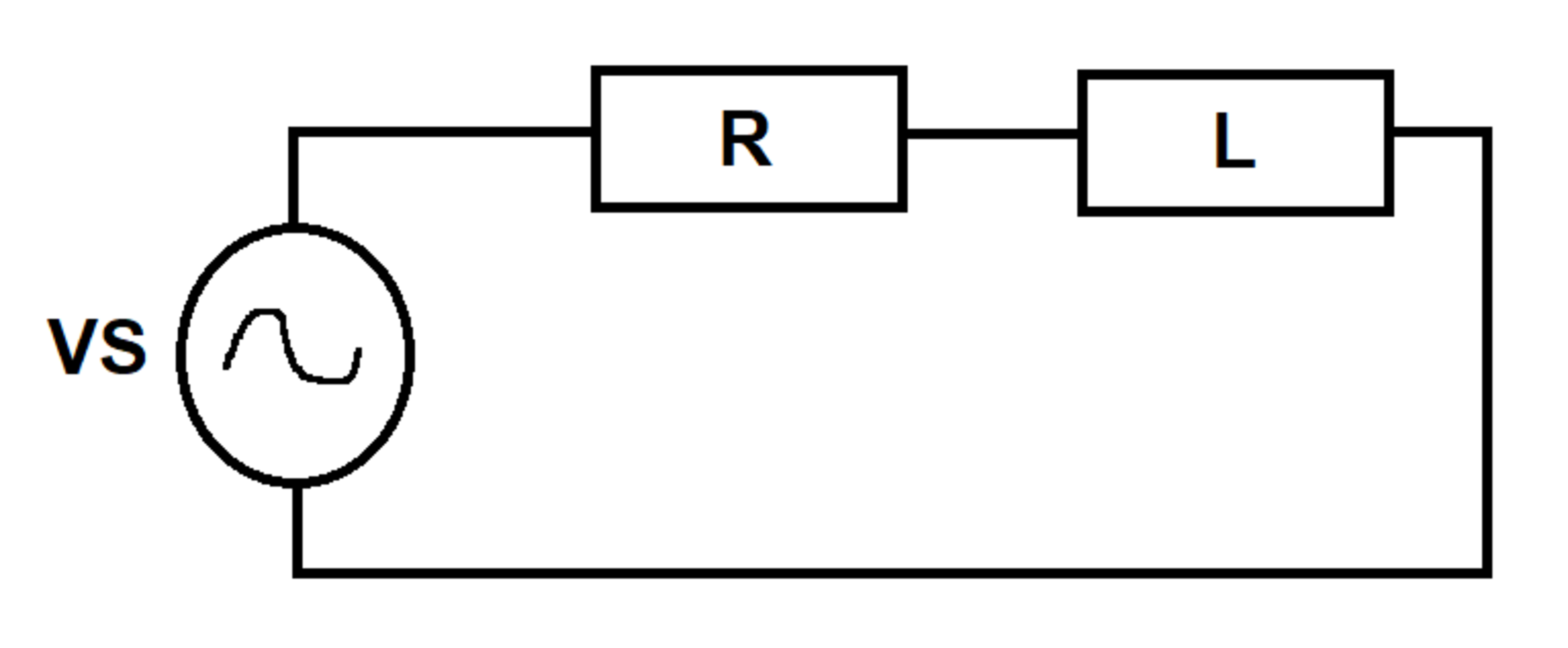
Basic RL Transient

Per KVL, the $RL$ circuit follows the ODE:

$Li'(t) + Ri(t) = V_{S}(t) \Rightarrow i'(t) + 0.1i(t) = \sin(t), i(0)=0$ .

By Laplace Transforms, we obtain:

$sI(s) + i(0) + 0.1I(s) = \frac{1}{s^2+1} \Rightarrow I(s) = \frac{1}{(s+0.1)(s^2+1)}$ ,

and taking the inverse L.T. gives:

$i(t) = 0.99e^{-0.1t} + 0.099\sin(t) - 0.99\cos(t)$

which has the plot for $t \g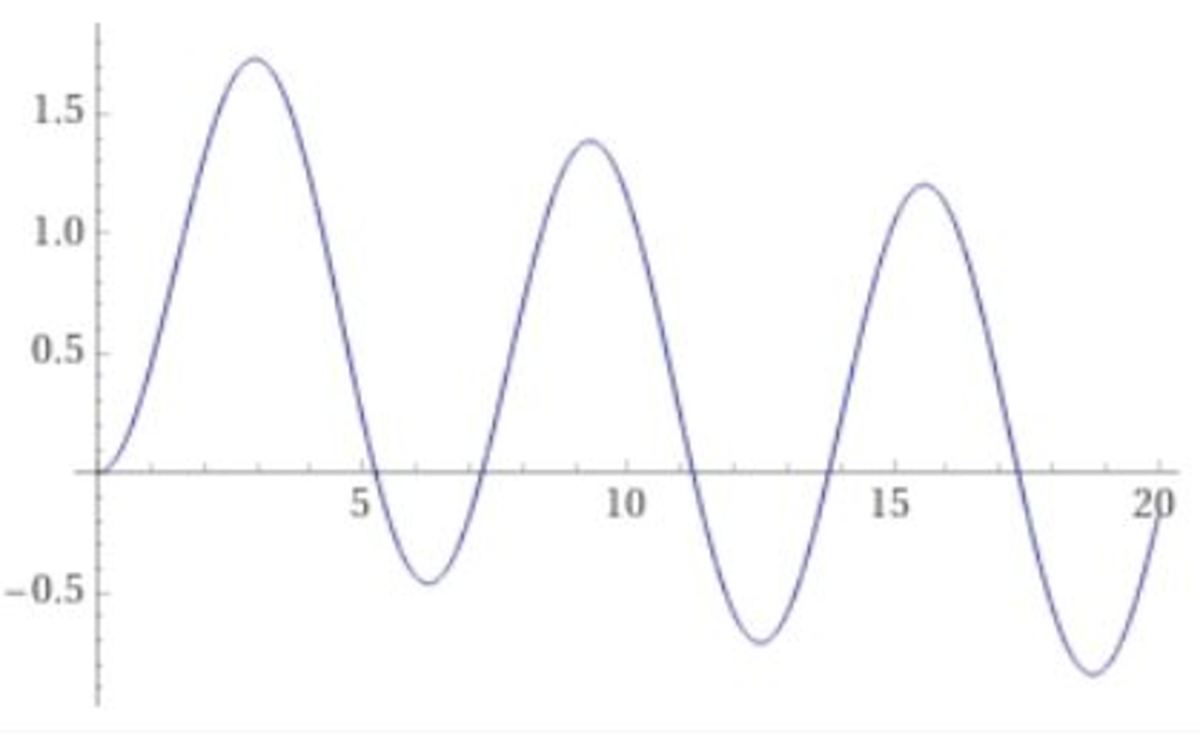e 0:$

Taking the first derivative of the current and setting equal to zero yields:

$i'(t) = -0.099e^{-0.1t} + 0.099\cos(t) + 0.99\sin(t) = 0 \Rightarrow t = 2.968$ ,

which is the time value of the first local maximum current value. A quick check of this value at the second derivative gives: $i''(2.968) = -0.985 < 0$ , which is a maximum value. So the maximum instantaneous current computes to $i(2.968) = \boxed{1.72798}$ amps.