Basing 3 and 4

If the digit sum of $n$ in base $3$ is $3$ then

$n=3^a+3^b+3^c\qquad a,b,c\in\mathbb{N}$

Where at most $2$ of $a,b,c$ are equal. In a similar way

$n=4^d+4^e\qquad d,e\in\mathbb{N}$

Hence

$3^a+3^b+3^c=4^d+4^e$

The $LHS$ is always odd, so w.l.o.g. $e=0$ . Since the $RHS$ is always $2 \mod 3$ , we need to have $b=c=0$

$3^a+1=4^d$

By Mihăilescu's theorem, the only solution is $a=d=1$ .

This gives $n=5=12_3=11_4$ as the only solution

Remembering that if $x$ has digit sum $y$ in base $b$ then $x \equiv y \mod b-1$ . Thus, $a \equiv 1 \mod 2, a \equiv 2 \mod 3$ . By CRT, these are equivalent to $a \equiv -1 \mod 6$ .

Now, as $a$ has digit sum $3$ in base 3, it either has a 1 and a 2 in its digit expansion, or three 1's. In the latter case we would have that $a = 3^x + 3^y + 3^z \equiv -1 \mod 6$ ( $x \neq y \neq z$ ). It is a trivial computation to check that a solution to this congruence would have $y=z=0$ which is a contradiction. So it must be that $a = 3^x + 2 \times 3^y \equiv -1 \mod 6$ . Again, it is a trivial computation to find that solutions only occur when $y = 0$ . So $a = 3^x + 2$ .

On the other hand $a$ has digit sum $2$ base 4 so it has either two 1's in its expansion or just a 2. In the latter case we would have $a = 2 \times 4^x \equiv -1 \mod 6$ . This congruence has no solutions. So it must be that $a = 4^x + 4^y \equiv -1 \mod 6$ . A solution is only possible if $y = 0, x \neq 0$ . So $a = 4^x + 1$ .

We now have to solve the diophantine equation $3^y + 2 = 4^x + 1$ Rewrite as $3^y = 2^{2x} - 1 \implies 3^y = (2^x - 1)(2^x + 1) \implies 2^x - 1 = 3^a, 2^x + 1 = 3^b \implies 2^{x+1} = 3^a + 3^b \implies$ that either $a$ or $b$ has to be zero (if both are non-zero then LHS is divisible by 3, which is a contradiction). Check both cases to obtain the only solution, $x=y=1$ which means $a=5$ .

To see why the congruences I studied behave like I mention notice that $3^x \equiv 3 \mod 6$ and $4^x \equiv 4 \mod 6$ for $x>0$ . And $3^0 \equiv 4^0 \equiv 1 \mod 6$ .

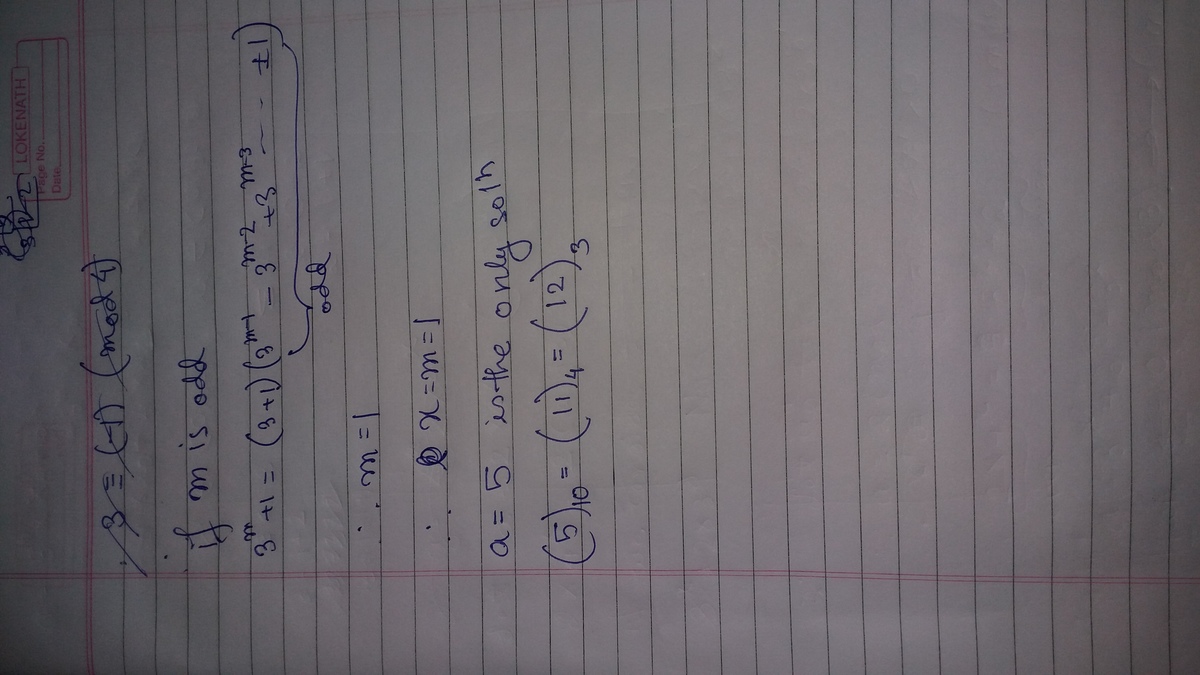Sorry for the picture being like this...could not make it straight :(