Baumkuchen

Calculus Level 3

A baumkuchen or split cake has a hollow unit circular area in the middle with successive ring with the same unit radius, in which the first ring is divided equally in 6 portions, second ring in 12, third ring in 18, and so on, as shown below:

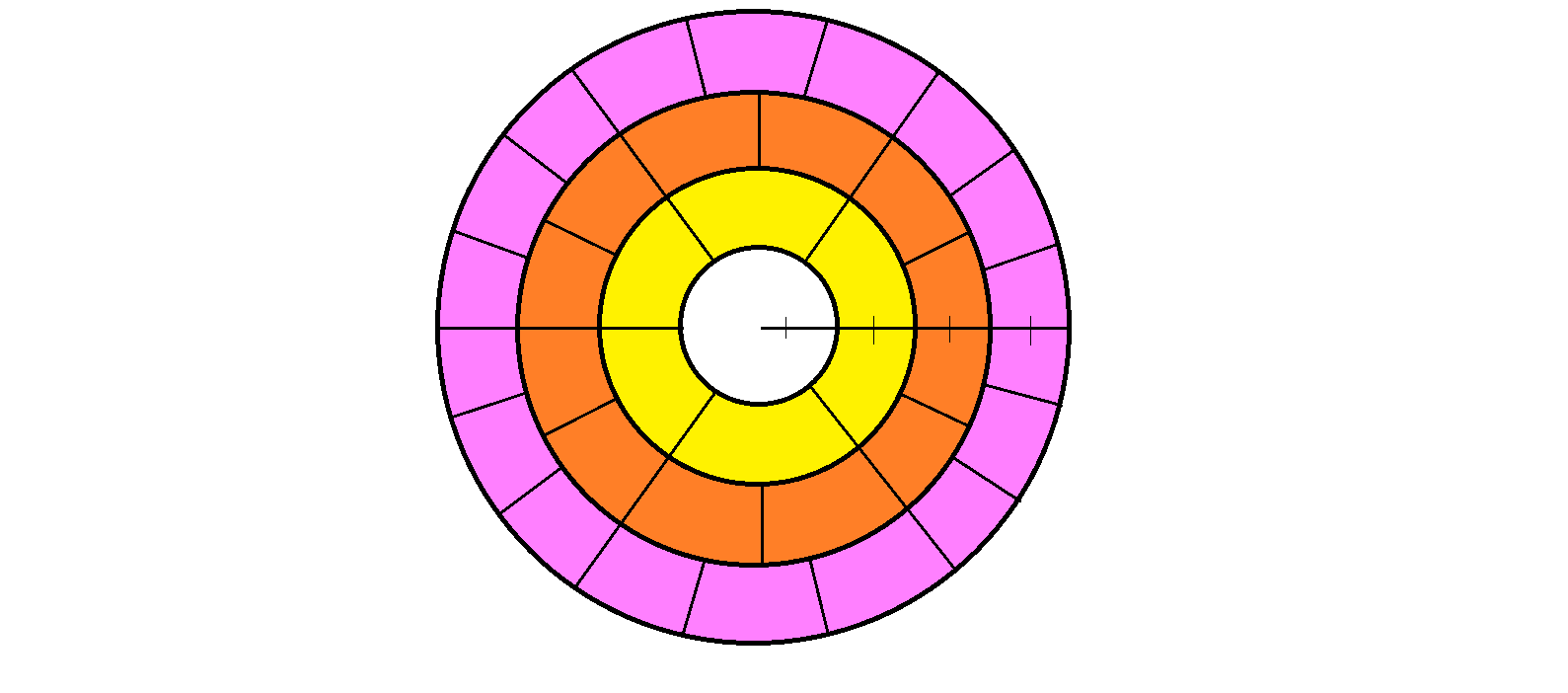
As the ring progresses infinitely, what is the area ratio of the unit circle to each portion of the $n^{th}$ ring?

The answer is 3.

1 solution

Worranat Pakornrat
Jun 10, 2017

The area of the $n^{th}$ ring = $\pi(n^2) - \pi(n-1)^2 = \pi(2n+1)$ .

The division progresses as an arithmetic sequence of $6n$ . Thus, each portion of $n^{th}$ ring = $\dfrac{\pi(2n+1)}{6n}$ .

As a result, the area ratio = $\lim_{n\to\infty} \dfrac{\pi}{\dfrac{\pi(2n+1)}{6n}} = \lim_{n\to\infty} \dfrac{6n}{2n+1} =\boxed{3}$ .

I believe that, by your logic, the area of the n-th ring is π(2n-1). But your flaw is that the n-th ring does not have radius n. Instead it has radius n+1. So the area of the n-th ring is π(n+1)^2 - πn^2=π(2n+1). That's because the 1st ring is the yellow ring, which has a radius of 2.

maximos stratis - 3 years, 12 months ago

Well, it doesn't really matter. With limit to infinity, it will yield the same result, right? :)

Worranat Pakornrat - 3 years, 12 months ago

Of course but just for the sake of being totally right :P

maximos stratis - 3 years, 12 months ago

Baumkuchen

The answer is 3.

1 solution

0 pending reports