BdMO 2014 Problem

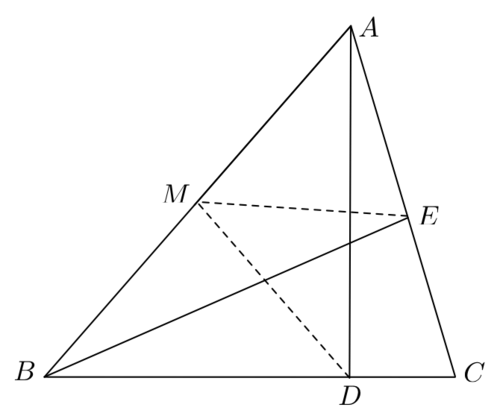We can find that angle EAD and angle EBD are of 30° so we can cinstruct a circle with ED as a chord and passing through A and B. Now, as angle AEB is 90°, thus AB is the diameter and M the centre. Thus angle EMD is 60°

Let H be the orthocentre of the triangle ABC. Clearly, HECD is cyclic(since E+D=9+90=180)

Let O be the centre of the quad EHCD. Clearly, angle EOD=120(twice to that of ECD)

We know that, EODM is cyclic (since E,O,D,M are points on the nine point circle)

therefore, angleEMD + ange EOD = 180 which gives that EMD=60

$\angle BDA\quad =\quad \angle AEB\quad =\quad 90°$ These are angles subtended by chord AB on a circle which passes through A, E, D and B. Since the angles are equal to 90°, AB is the diameter of the circle i.e M is the centre. Now we know that $\angle C$ = 60°. Therefore $\angle EBC$ = 30°. Now consider chord ED. We know that the angle subtended by the chord at centre is equal to twice the angle subtended by the same chord anywhere in the same part of the circle. So, $\angle EMD$ = 2 $\angle EBC$ = 60°.

Since perpeiculars make 90 degree and angle BCA is 60 degree given,angles CAD AND CBE are 30 degree.. Since M is middle point of AB ,AMD becmes equlateral trianle and therefore all anles are 60 degree .So, angle EMD is 60 degrees Ans

K.K.GARG.India

It's a natural consecuence of the 9 points circunference theorem. However, this is like killing a fly with a bazooka.

60 degrees.. since, the angle M must b same 4 any triangle with c=60 dgree.. consider a equlatrl triangl wit all angle equals 60 dgree... 4 equ triangle, perpendicular,median and angle bisectors are same. thus by using these proptys angle m=60 dgree

Sorry for the picture quality.

If bisector AD and Be is P. I just see congruen between APE and BPD is congruen.. So ABC is triangle with the same leght.. It mean EMD is pedal of ABC wich have measure is 60

For the perpendicular bisector of AC to pass through B, angle BAC must be equal to angle BCA which is 60 degrees, leaving 60 degrees for angle ABC. Hence, ABC is an equilateral triangle. If AD is perpendicular to BC, it must also bisect it (because the triangle ABC is equilateral). As, M, E and D are the midpoints of each side of the equilateral triangle, it follows that triangle MED is also an equilateral and angle EMD is 60 degrees.

As BE is a perpendicular on AC so CEB=90 and C=60 so EBC=30 again as AD is a perpendicular on BC so ADB=90 now lets consider P and Q are points on MD and AD respectively as BP and MQ are perpendiculars on MD and AD respectively.As BP a perpendicular MD so BPD=90 and EBC=PBD=30 thus in triangle BPD, BDP=60.Now QDM=ADB-BDP=90-60=30.Again as MQ a perpendicular on AD so MQD=90 and QDM=30 so in triangle QMD, DMQ=60 which means EMD=60

we can draw a circle with m as centre and the circle passes through a,b,d,e........ then u can solve it

Since Traingle BCE and Triangle BEA are both right triangles and given that angle C is 60 deg, Special Triangles (30-60-90) is applicable to determine angle EMD.

Regardless of the illustration, Triangle ABC is an equilateral triangle with side 2, and since M is the midpoint of side AB, therefore side BM is 1. Since angle EBC and angle ABE are both 30 deg, therefore angle B = 30 deg + 30 deg = 60 deg and Side BD is 1. With that, Triangle BMD is also an equilateral triangle with side 1.

Since angle BMD and AME are both 60 degrees and a straight angle measures 180 deg, therefore angle EMD is equal to 60 deg.

Thales theorem teaches us that when 2 triangles have the same angle and a commom side they are similar, thus their angles are equal therefore it is a matter of re-arranging the triangle to fit with the known 90 º and we find that EMD is in the place of the 60

we can see ME=MA and MD= MB.so <AME=180-2 <A and <BMD=180-2<B.we also have <A+<B=120,which gives <EMD=60

Clearly, quadrilateral $AECB$ is cyclic and $AB$ is the diameter of the circumscribing circle. $M$ is the midpoint of $AB$ means that $M$ is the centre of the circumscribing circle. Now, in $\triangle ACD$ , $\angle C = 60^{\circ}$ and hence $\angle CAD = \angle EAD = 90^{\circ} - 60^{\circ} = 30^{\circ}$ . Now $\angle EMD = 2 \angle EAD = \boxed{60^{\circ}}$