BdMO(Regional) 2012 Problem
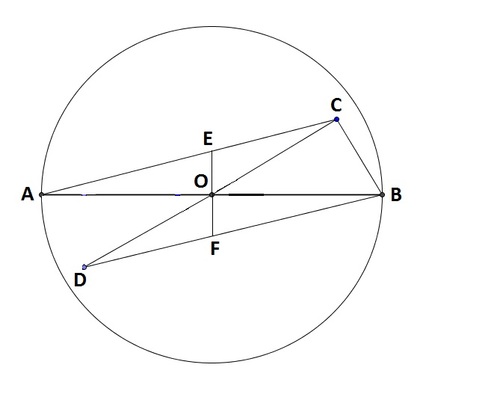 In a circle,
A
B
=
4
is the diameter and
O
is the centre.
C
and
D
are chosen such that
C
,
O
,
D
are co-linear,
∠
C
O
B
=
∠
A
O
D
=
3
0
∘
,
O
C
=
O
D
and
∠
B
C
O
=
9
0
∘
. The perpendicular on
A
B
through
O
meets
A
C
at
E
and
B
D
at
F
.
In a circle,
A
B
=
4
is the diameter and
O
is the centre.
C
and
D
are chosen such that
C
,
O
,
D
are co-linear,
∠
C
O
B
=
∠
A
O
D
=
3
0
∘
,
O
C
=
O
D
and
∠
B
C
O
=
9
0
∘
. The perpendicular on
A
B
through
O
meets
A
C
at
E
and
B
D
at
F
.
If E F = c a b where a , b , c are integers and b , c are primes, find the value of a + b + c .
Note: C and D are not necessarily on the circumference of the circle.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
After finding CM = SQRT(3)/2 and OM = 3/2, consider the similar triangles AEO & ACM
EO/CM = AO/AM = 2/(3/2)....EO/{SQRT(3)/2}.....2
EO = 2SQRT(3)/(2 + 3/2)
EF = 2
EO = 2SQRT(3)/( 7/2) = 4SQRT(3)/ 7
Log in to reply
WE SHOULD HAVE
EO/CM = AO/AM = 2/( 2+3/2) = .EO/{SQRT(3)/2}.
SORRY FOR THE MISTAKE.
\boxed[14]
(Please consider Fahin points names above to follow my solution)
Triangle B C O is a "half-equilateral-triangle" with "side" B O = 2 (radius). So, B C = 1 ("half-side") and C O = 3 .
Because C M is a height of right triangle B O C , we know B O ⋅ C M = C B ⋅ C O and then we get C M = 2 3 . Applying Pythagorean Theorem at triangle C O M , we get O M = 2 3 . Thus, A M = 2 7 .
Triangles AEO and ACM are similar, so C M E O = A M A O and we get E O = 7 2 3 . Since the symmetry of given construction, E F = 2 E O , therefore, E F = 7 4 3 and the answer is 4 + 3 + 7 = 1 4 .
Try my geometry classic question Find the area . I'm sure u will enjoy this
For convenience, I would also like to borrow Shakkhor's diagram.
If ∠ C O B = 3 0 ∘ and ∠ O C B = 9 0 ∘ , then △ C O B is a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle with O B as its hypotenuse and C B as the short leg. 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangles are a special kind of right triangle in that the measurement of the short leg is half of that of the hypotenuse and the measure of the longer leg is that of the short leg multiplied by 3 . Since O B is a radius of ◯ O which has a diameter of 4 , O B = 2 , and since O B is the hypotenuse of △ C O B , m C B = 2 m O B = 2 2 = 1 and m O C = m C B × 3 = ( 1 ) ( 3 ) = 3 .
Let us construct point M such that O B ⊥ C M . Now, △ C O M is also a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle with O C as the hypotenuse and C M as the short leg. Since m O C = 3 , m C M = 2 m O C = 2 3 and m O M = m C M × 3 = ( 2 3 ) ( 3 ) = 2 ( 3 ) 2 = 2 3 .
Consider triangles △ A M C and △ A O E . Since ∠ A ≅ ∠ A and ∠ A M C ≅ ∠ A O E , △ A M C and △ A O E are similar triangles. We can assume that the ratios of A M to M C and A O to O E are the same as they are corresponding sides of similar triangles. A O is another radius of ◯ O so A O = O B = 2 . From the above, we can do the following:
m A M m M C ( m A O + m O M ) m M C 2 + 2 3 2 3 2 4 + 2 3 2 3 2 7 2 3 ( 2 3 ) ( 7 2 ) 7 3 7 2 3 = m A O m O E = m A O m O E = 2 m O E = 2 m O E = 2 m O E = 2 m O E = 2 m O E = m O E
We now know how long O E is. But to find the length of E F , we have to find first m O F . Looking at the diagram, we can get a hunch that O E ≅ O F . Consider triangles △ A O C and △ B O D . ∠ A O C and ∠ B O D are vertical angles formed by the intersection of A B and C D and thus ∠ A O C ≅ ∠ B O D . Also, we already know that C O ≅ D O and A O ≅ B O . By that, △ A O C and △ B O D are congruent (by S A S congruence) and ∠ A C O ≅ ∠ B D O . Further, consider triangles △ E O C and △ F O D . Since the sets of points C , O , and D , and E , O , F are collinear, then ∠ E O C and ∠ F O D are vertical angles and are congruent to each other. It is already known that C O ≅ D O . Finally, ∠ A C O ≅ ∠ E C O , ∠ B D O ≅ ∠ F D O and ∠ A C O ≅ ∠ F D O . Thus, △ E O C and △ F O D are congruent (by A S A congruence) and E O ≅ F O .
Thus, m E F = m E O + m O F = m E O + m E O = 7 2 3 + 7 2 3 = 7 4 3 . Finally, a = 4 , b = 3 , c = 7 and a + b + c = 4 + 3 + 7 = 1 4 .
Too long !!
EF=(4√3)/7 a + b + c = 4 + 3 + 7 = 14
- Join D to A. Since, ∠COB = ∠AOD with DO = OC and AO = OB; AD = CB and AC = DB.
- Thus, △AOD and △COB are congruent triangles. Also, △AOC and △DOB are congruent. So, ∠ODA = ∠BCO = 90° or AD||BC. Also, ∠CAO = ∠OBD. This indicates that AC and BD are parallel. Hence, ACBD is a parallelogram. Thus, AD=BC and AC=BD. From ∟△AOD, ∠OAD = 60° (Since, ∠AOD = ∠COB = 30°). In a 30°:60°:90° triangle, the sides are in the ratio 1:2:√3. Given AB=4, AO=OB=2. Also given, OC=OD = √3. Thus, AD = CB = 1.
- Now, drop a perpendicular from D to AB say DX. From ∟△ADX, cos30°= DX/1 or DX = (√3)/2. By Pythagorean theorem, AX = 1/2. Thus, XB = 3.5 or 7/2.
- From ∟△DBX, by Pythagorean theorem, DB = √((7/2)^2+((√3)/2)^2) = √13.
- Since, OF||XD, by AAA theorem, ∟△BOF and ∟△BXD are similar triangles. Thus, BO/BX = BF/BD = OF/XD or 2/3.5 = BF/√13 = OF/(√3/2). This gives, OF = (2√3)/7.
- Since ACBD is a parallelogram, with points E, O and F being collinear, OE=OF.
- Hence, EF = 2OE = 2OF = 2((2√3)/7) = (4√3)/7 = (a√b)/c. a, b, c are integers and b, c are primes.
- Or, a+b+c = 14.
EF=(4√3)/7 a + b + c = 4 + 3 + 7 = 14
Easy solution: Find CO through pitagoras in COB then find AC through cossine law in AOC. Call the area from EOC as A1 and the area of EOA as A2. A1 is the product of EOxOCxsin60º/2, and that makes 3/4xY, beeing Y the half of EF. A2 is AOxY/2, and that makes Y. We know now that the area of the triangle AOC is 7xY/4, but this same area can be found by multiplying AOxOCxsin(150)/2, and that makes sqrt(3)/2. So, we know that 7xY/4 is equal to sqrt(3)/2. Doing the math we find that Y = 2xsqrt(3)/7, and EF is 2xY. So EF is 4xsqrt(3)/7. a = 4, b = 3 and c = 7. The sum makes 14.
Since OB=2, and angles COB=30^ & CBO=60^, sines of these angles give CB=1 & OC=Sqrt 3. Now, in triangle AOC, the sum of angles OAC & OCA is 30^. Since angle ACD & CDB are equal therefore angle OAC = 30^-CDB. In triangle CDB, the base CD is 2 SQRT3, thus tan CDB=1/2 SQRT 3. Now, tan CAO= TAN (30^-CDB)=(1/SQRT 3 -1/2 SQRT 3)/(1+ 1/SQRT3 * 1/2 SQRT3) = SQRT3/7 = EO/AO. This yields EO=2 SQRT 3/7.... and since EF=2 EO, therefore it comes to be 4 SQRT 3/ 7. equating 4,3 & 7 with the unknowns a, b & c, we get the sum 4+3+7=14.
In △ B O C , sin O B C = O B O C → sin 6 0 ∘ = 2 O C → O C = 3
Draw a perpendicular C M from point C on A B .
In △ O C M , sin C O M = O C C M → sin 3 0 ∘ = 3 C M → C M = 2 3
cos C O M = O C O M → cos 3 0 ∘ = 3 O M → O M = 2 3
In △ A C M , A C 2 = A M 2 + C M 2 = ( O A + O M ) 2 + C M 2 = ( 2 + 2 3 ) 2 + ( 2 3 ) 2 = 4 4 9 + 4 3 = 1 3
A C = 1 3
In △ A O C , sin A O C sin x = A C O C → sin x = 1 3 3 × sin 1 5 0 ∘ → sin x = 2 1 3 3
cos x = 1 − s i n 2 x = 1 − 5 2 3 = 5 2 4 9 = 2 1 3 7
tan x = cos x sin x = 7 3
tan x = O A O E → O E = O A tan x → O E = 2 7 3
E F = 2 O E = 4 7 3
4 + 3 + 7 = 1 4