BE smart
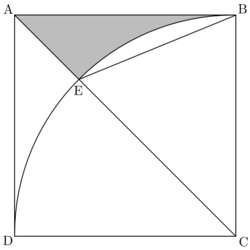 A square
A
B
C
D
has an inscribed quadrant with centre
C
. Let
E
be the point inside the square where the diagonal
A
C
and arc
B
D
intersect. The area of the shaded section is
1
2
1
.
A square
A
B
C
D
has an inscribed quadrant with centre
C
. Let
E
be the point inside the square where the diagonal
A
C
and arc
B
D
intersect. The area of the shaded section is
1
2
1
.
Find the ceiling of the length of B E .
Created by Michael Fuller . Popular geometry problems: "Star Stumper" , "Not your average shuriken"
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let x be equal to the side of the square. Due to symmetry, we can say that the area of the square minus the area of the quadrant of the circle is equal to double the area of the shaded section, i.e.
x 2 − 4 π x 2 = 2 4 2 ⇒ x 2 ( 1 − 4 π ) = 2 4 2 x = 1 − 4 π 2 4 2 ≈ 3 3 . 5 8 1
Consider △ B E C . Line segments E C and B C are both radii of length x so the triangle is isosceles. Using the sine rule we have
sin 6 7 . 5 ° x = sin 4 5 ° B E B E ≈ 2 5 . 7 0 2 ⌈ B E ⌉ = 2 6
Let x = A B = B C = C D = A D . By Pythagoras, A C *= x 2 . Then, E C = B C since E C is a radius, and since A C = x 2 , so A E = x 2 − x . Let M be a point in A B such that A B ⊥ M E as shown in the figure. Note that △ A M E is an isosceles triangle with ∠ E A M = ∠ A M E = 4 5 ∘ . This implies, by Thales, that M E = A M = x − 2 2 x and M B = 2 2 x . Once again, by Pythagoras in △ M E B , B E = x 2 ( 2 − 2 ) . In order to find x , it is known that area of A B C D = x 2 , but from a different perspective, note that shaded area is 121 and the whole area outside the circumference is 242. Area of quadrant of the circumference is 4 x 2 π , we have the following equation: x 2 = 2 4 2 + 4 x 2 π Hence, x 2 = 4 − π 9 6 8 . Replacing this in B E , we have that B E ≈ 2 5 . 7 0 1 6 . . . . Thus, ⌈ B E ⌉ = 2 6 .