Be Sure to Meet

Algebra Level 2

Suppose that m m is a real number such that the two graphs 2 ∣ x − 1 ∣ + ∣ y ∣ = 2 and y = m x + 5 m − 2 2|x-1|+|y|=2\ \text { and } y=mx+5m-2 intersect. What is the sum of the maximum and minimum values of m ? m?

3 4 \frac{3}{4} 1 2 \frac{1}{2} 2 3 \frac{2}{3} 4 5 \frac{4}{5}

View wiki
Mahindra Jain by Mahindra Jain

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tom Engelsman
Nov 22, 2020

The plot of 2 ∣ x − 1 ∣ + ∣ y ∣ = 2 2|x-1| + |y| =2 is a rhombus: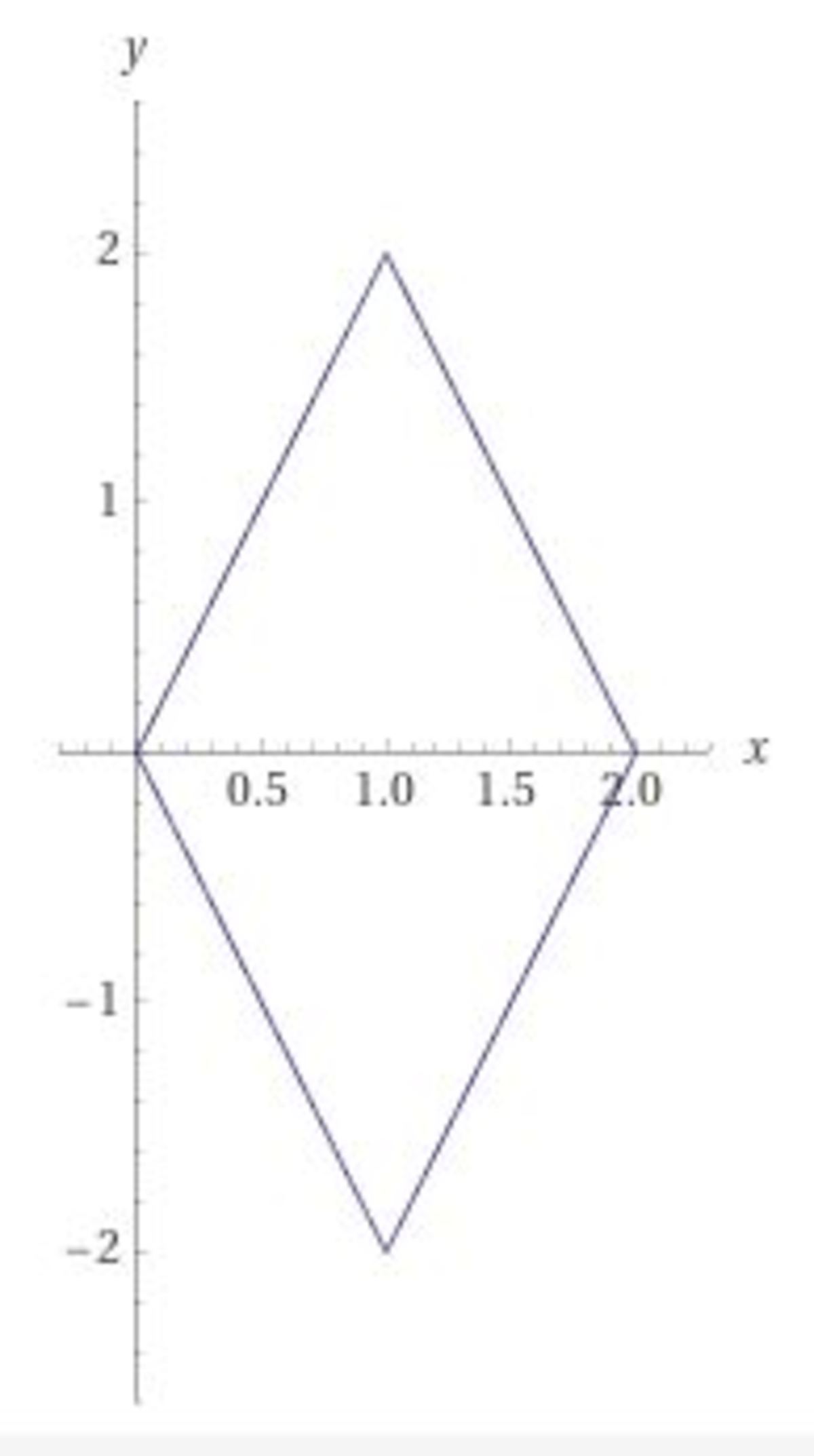

with vertices at ( x , y ) = ( 0 , 0 ) ; ( 1 , − 2 ) ; ( 1 , 2 ) ; ( 2 , 0 ) (x,y) = (0,0); (1,-2); (1,2); (2,0) . Solving for m m gives m ( x , y ) = y + 2 x + 5 m(x,y) = \frac{y+2}{x+5} , and if we substitute the aforementioned points we obtain:

m ( 0 , 0 ) = 2 5 ; m ( 1 , − 2 ) = 0 ; m ( 1 , 2 ) = 2 3 ; m ( 2 , 0 ) = 2 7 . m(0,0) = \frac{2}{5}; m(1,-2) = 0; m(1,2) = \frac{2}{3}; m(2,0) = \frac{2}{7}.

Hence, m M I N + m M A X = 0 + 2 3 = 2 3 . m_{MIN} + m_{MAX} = 0 + \frac{2}{3} = \boxed{\frac{2}{3}}.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...