Obtaining The Right Amount Of Mixture
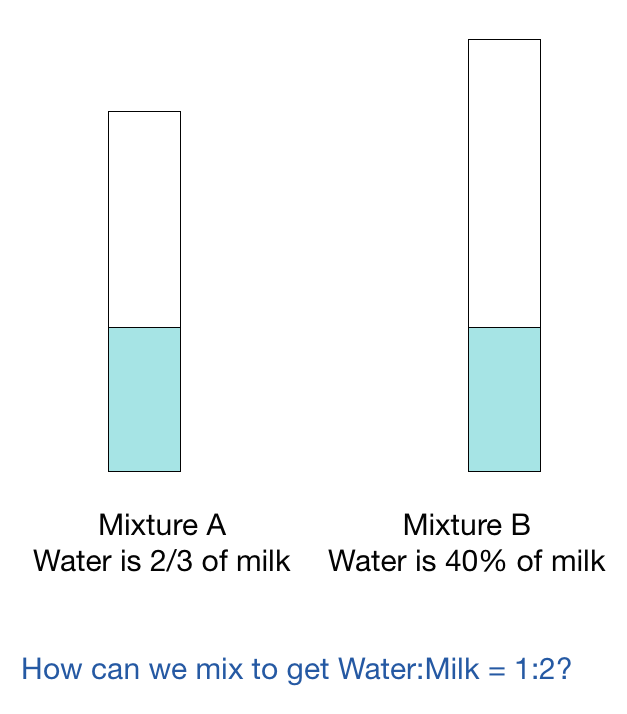
There are two vessels containing the mixture of milk and water. In the first vessel the water is of the milk and in the second vessel water is just of the milk. In what ratio should we mix these liquids to obtain a mixture with a water to milk ratio of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the first vessel, concentration of water is 3 5 3 2 = 5 2 .
In the second vessel the concentration of water is 7 2 .
The resultant mixture should have a water concentration of 3 1 .
By allegation method, they will combine in the ratio of 2 1 1 : 1 5 1 = 1 5 : 2 1 = 5 : 7 .