Beach on the highway
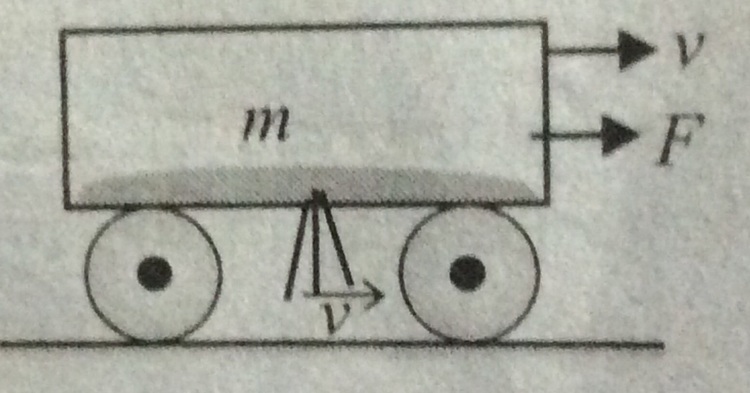
 A cart loaded with sand moves along a flat, straight track due to a constant force
parallel to the cart's velocity vector. The sand spills through a hole in the bottom at a constant rate
kg/s .
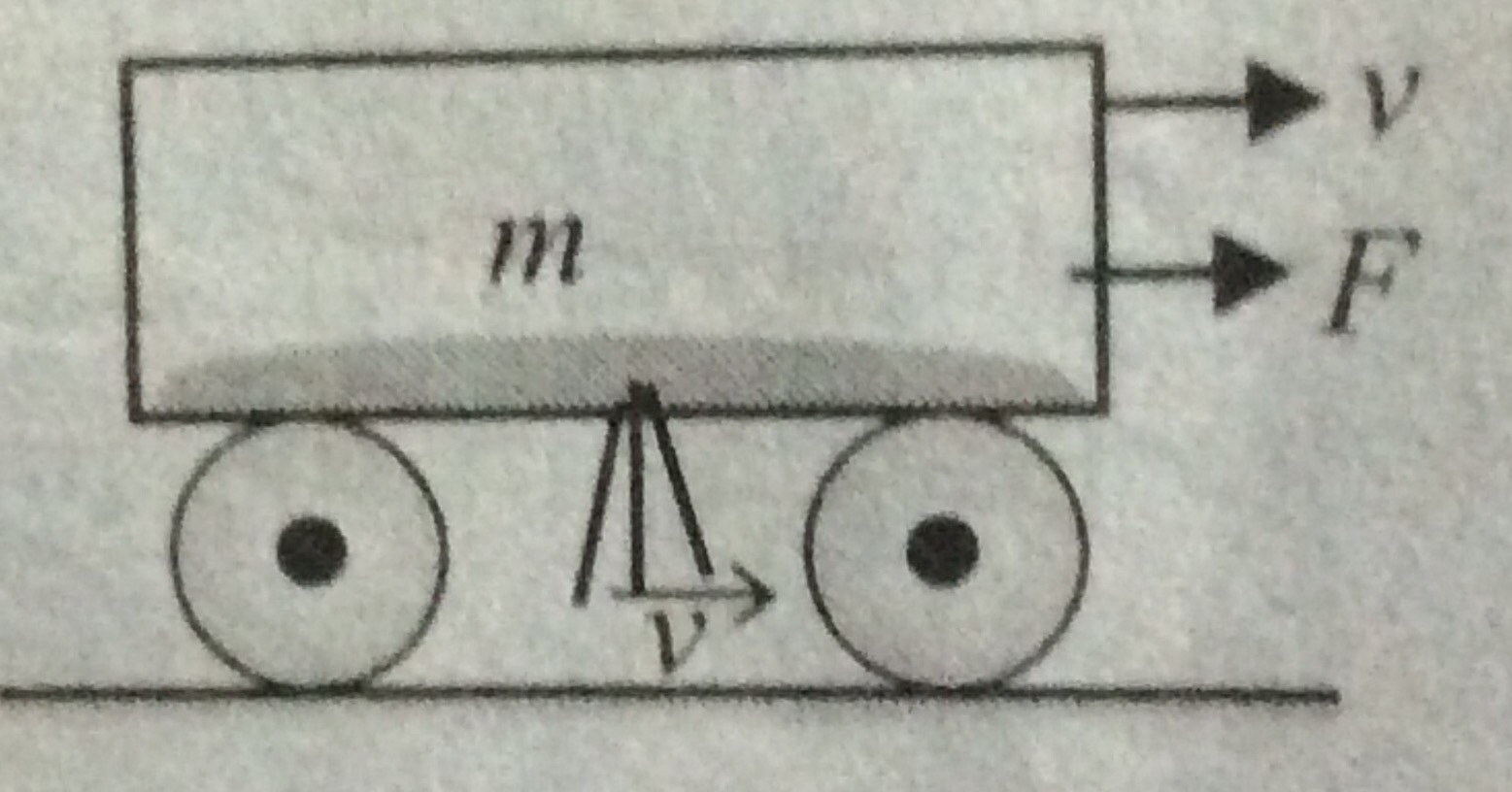
A cart loaded with sand moves along a flat, straight track due to a constant force
parallel to the cart's velocity vector. The sand spills through a hole in the bottom at a constant rate
kg/s .
Find the time when the velocity of the cart will be given that velocity of cart at is zero, and the initial mass of the cart is .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
a=F/(M-zt)=dv/dt integrating this equation with v=0 to F/z and t=0 to t we get the answer