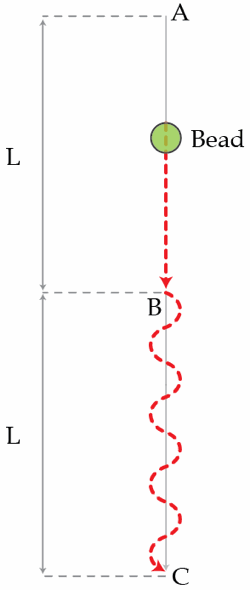
Bead on a wavy wire

Straight section

In the first segment of the wire, the bead is in free fall under the influence of gravity. It takes the bead time

$t_1 = \sqrt{2L/g}$ (by conservation of energy: $\frac12 mv^2=mgh$ )

to fall this distance and exits the section with the speed

$v_1 = \sqrt{2gL}$ (by kinematics: $\frac12 gt^2 = L$ ).

Wavy section

In the wavy section, the key is to recognize that the detailed kinematics of the bead at any moment is irrelevant to the time taken, $t_2$ .

As the bead moves along the curve of the wire, it is subject to a changing acceleration which varies from $g$ whenever the wire turns around, to $g\cos\theta_c$ where $\theta_c$ is the angle between the wire and the vertical at the inflection points of the wire's curve.

This, however, does not matter. What does matter is the average acceleration that the bead experiences along the path. Regardless of the path that is actually taken by the bead, it must achieve a vertical drop of length $L$ and travel a path distance of length $2L$ which means it must have the same average acceleration as every other path which drops a vertical distance $L$ while traveling a path length $2L$ . We can therefore calculate using a simpler path with the same average acceleration.

In particular, we can map the path of the wavy wire onto an inclined plane of height $L$ with hypotenuse of length $2L$ .

image

Now we simply have a particle which enters an inclined plane with some initial velocity $v_1$ and accelerates along the inclined plane with the acceleration $a = g\sin\theta$ , with the angle $\theta$ given by $\sin\theta = \frac12 \rightarrow \theta = \frac{\pi}{6}.$

Therefore, we have

$\displaystyle v_1 t_2 + \frac12 g \sin\theta t_2^2 = 2L$

which gives $\begin{aligned} t_2 &= \frac{\sqrt{4gL\sin\theta+v_1^2}-v_1}{g\sin\theta}\\ &= \frac{\sqrt{4gL\sin\theta+2gL}-\sqrt{2gL}}{g\sin\theta}\\ &= \sqrt{16L/g}-\sqrt{8L/g} \end{aligned}$

Giving an overall time of

$\displaystyle \boxed{t_1+t_2 = \sqrt{L/g}\left(\sqrt{2} + \sqrt{16}-\sqrt{8}\right)\approx 0.584 \mbox{ seconds}}$

The speeds of the bead at B and C respectively are: $v_1= \sqrt{2gL}$ and $v_2=\sqrt{4gL}$ .

The time it takes for the bead to reach B is: $t_1=\sqrt{\frac{2L}{g}}$ .

The wavy section BC is totally similar to a straight line with length 2L and height L, so the acceleration of the bead in this section is $a=\frac{gL}{2L}=\frac{g}{2}$ .

The time it takes in section BC is: $t_2=\frac{v_2-v_1}{a}=\sqrt{\frac{L}{g}}(4-2\sqrt2)$ .

The total times are: $t=t_1+t_2=\sqrt{\frac{L}{g}}(4-\sqrt2)=0.584(s)$ .

We need to treat the two portions of the wire separately, since the accelerations of the bead in each section will be different.

Conservation of energy tells us when the bead is at the end of the straight section, it has speed $v_1=\sqrt{2gL}$ . Since it started at rest, and has constant acceleration, its average speed for the straight portion must be half of that value, $v_{avg}=\sqrt{\frac{gL}{2}}$ and the time to get to that point must be $\Delta t_1=\frac{L}{v_{avg}}=\sqrt{\frac{2L}{g}}$ .

Similarly, conservation of energy tells us when the bead is at the bottom of the wire, it has speed $v_2=\sqrt{4gL}$ . Since it began this portion with a speed of $v_1=\sqrt{2gL}$ , and has constant acceleration, its average speed over that range must be $v_{avg}=\frac{v_1+v_2}{2}=(1+\frac{\sqrt{2}}{2})\sqrt{gL}$ .

Since the bead travels a distance $2L$ with that average speed, the time to cover that length must be $\Delta t_2=\frac{2L}{v_{avg}}=\frac{4L}{(2+\sqrt{2})\sqrt{gL}}$ .

The total time is just $\Delta t_1+\Delta t_2$ , which simplifies to $(\frac{4}{2+\sqrt{2}}+\sqrt{2})\sqrt{\frac{L}{g}}\approx0.584$ seconds.

First, compute the time it takes for the bead to go from $A$ to $B$ : $\Delta x=-\frac12gt_{AB}^{2}=L$ $\Rightarrow t_{AB}=\sqrt{\frac{2L}{g}}$ We know that by the conservation of energy, the velocity ( $v$ ) is related to the height ( $h$ ) of the bead above point $C$ by $\frac{1}{2}mv^{2}+mgh=2mL$ From here we can solve for $v$ and a function of $h$ : $v=-\sqrt{2g(2L-h)}\tag{1}$ Now if the wire were not wavy, then the time ( $t_{0}$ ) it would take for the bead to go from $B$ to $C$ can be found by writing $(1)$ as a differential equation, then separating and integrating: $\frac{\mathrm{d}h}{\mathrm{d}t}=-\sqrt{2g(2L-h)}$ $\Rightarrow t_0=\int_0^L \! \frac{\mathrm{d}h}{\sqrt{2g(2L-h)}}\tag{2}$ For the problem at hand, we can still use $(1)$ but $v$ is not $\frac{\mathrm{d}h}{\mathrm{d}t}$ , it is $\frac{\mathrm{d}s}{\mathrm{d}t}$ where $s$ is the length along the wavy curve that the wire makes. But $\mathrm{d}h$ and $\mathrm{d}s$ are related: if $h$ changes by a small amount, $s$ changes by twice that amount since the segment of the wire from $B$ to $C$ is compacted to half its normal size. So we have $\mathrm{d}s=2\mathrm{d}h$ Using this result and $(1)$ , we see that $t_{BC}=2\int_0^L \! \frac{\mathrm{d}h}{\sqrt{2g(2L-h)}}=2t_0$ Now we just need to find $t_0$ . We could evaluate ( $2$ ) but I chose to use the kinematic equation: $v_f=v_B+gt_0$ We know $v_f$ and $v_B$ from the conservation of energy. After finding $t_0$ , doubling it and adding $t_{AB}$ , we get $t_{BC}=2t_0+t_{AB}$ $=\boxed{.584 s}$

Imagine the race of two balls, ball 1 dropped vertically from rest at A and arrive at B below A height h, and ball 2 dropped from rest at A, roll on a slope of angle $\theta$ and arrive at B also below A height h.

$t_1 = \sqrt{\frac{2h}{g}}$ and $t_2 = \sqrt{\frac{2\frac{h}{sin\theta}}{gsin\theta}} = \frac{1}{sin\theta}\sqrt{\frac{2h}{g}}$

$\Rightarrow t_2 = \frac{t_1}{sin\theta} = t_1 \frac{l_2}{l_1}$ which $l_1$ and $l_2$ are lengths of the path which each balls travelled.

Apply to the problem, we got $t' = \sqrt{\frac{2\times 0.5}{g}} + 2\times (\sqrt{\frac{2\times 1}{g}} -\sqrt{\frac{2\times 0.5}{g}}) = 0.584 (s)$

Imagine the race of two balls, ball 1 dropped vertically from rest at A and arrive at B below A height h, and ball 2 dropped from rest at A, roll on a slope of angle and arrive at B also below A height h. and which and are lengths of the path which each balls travelled. Apply to the problem, we got Reply Subscribe to comments