Beam expansion through a telescope

Electricity and Magnetism Level 2

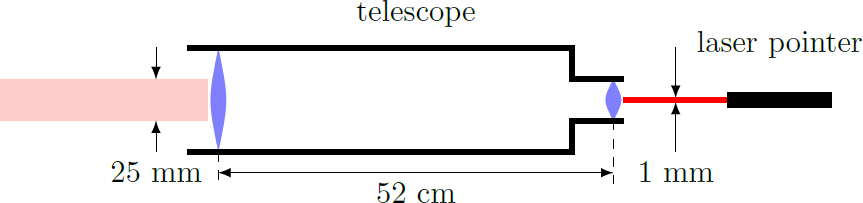
A laser beam is directed axially parallel through the ocular lens of a telescope. On the side of the objective lens, the laser beam emerges again as a parallel light beam. However, the beam diameter has widened from one millimeter originally to 25 millimeters. The length of the telescope (the distance between the ocular and objective lenses) is 52 centimeters.

What is the focal length of the ocular lens?

Assumptions: The telescope is a Keplerian telescope with two converging lenses. The thickness of each lens is negligible.

1 cm 2 cm 3 cm 4 cm 5 cm

1 solution

Markus Michelmann
Jun 9, 2018

In a telescope, which is used to image infinitely distant objects, the ocular and objective have a common focus. The distance between both lenses is therefore the sum of both focal lengths: $f_\text{ob} + f_\text{oc} = 52 \,\text{cm}$ An axial parallel beam through the eyepiece is focused in the common focus and converted by the objective lens back into a parallel beam. Due to the similarity of the triangles, the ratio of beam diameter and focal length must be the same on both sides of the focal point: $\frac{D'}{f_\text{ob}} = \frac{D}{f_\text{oc}} \quad \Rightarrow \quad f_\text{ob} = \frac{D'}{D} f_\text{oc} = 25 \cdot f_\text{oc}$
If we plug this into the first equation, we get the final result $f_\text{ob} + f_\text{oc} = 26 \cdot f_\text{oc} = 52 \,\text{cm} \quad \Rightarrow \quad \boxed{f_\text{oc} = 2 \,\text{cm}}$

Beam expansion through a telescope

1 solution

0 pending reports