Beam remains Parallel!
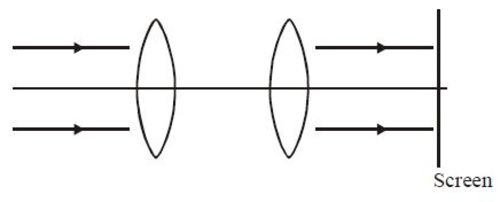 Two converging lenses of same aperture size are placed with their principal axis coinciding. Their focal lengths are in the ratio
. When a light beam is incident parallel to their common principal axis, it is observed that final emergent beam is also parallel to their common principal axis. It is observed that when beam is incident from left intensity recorded on screen is
, but when positions of lenses are interchanged, the same point on screen records an intensity
. Then
where
can have 2 values. Find the sum of the two values of
.
Two converging lenses of same aperture size are placed with their principal axis coinciding. Their focal lengths are in the ratio
. When a light beam is incident parallel to their common principal axis, it is observed that final emergent beam is also parallel to their common principal axis. It is observed that when beam is incident from left intensity recorded on screen is
, but when positions of lenses are interchanged, the same point on screen records an intensity
. Then
where
can have 2 values. Find the sum of the two values of
.
The answer is 0.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since no information is given to specifically distinguish I 1 and I 2 , they are interchangable. Therefore if x is a solution, so is − x :
I 1 I 2 = ( I 2 I 1 ) − 1 = ( K x 1 ) − 1 = K − x 1 .
Hence the sum of the two values must be x + ( − x ) = 0 .