Bean coloring

I will work my way to the given problem from simpler cases.

$P(x,y)$ =the probability of success if there are $x$ beans remaining of which $y$ are blue.

We seek $P(5,0)$ which is equivalent to $P(5,1)$ . In fact, $P(n,0)=P(n,1)$ is always true since if there are no blue we are guaranteed to pick a white and color it blue.

Also, $P(n,n)=0$ since if all the beans are blue we cannot succeed.

Some simple probabilities: $P(1,0)=1$ since this is the success condition. $P(2,1)=P(2,0)=\frac{1}{2}$ since having one white and one blue we can only succeed by picking the blue.

$P(3,2)=2/3*1/2=1/3$

$P(3,1)=2/3*P(3,2)+1/2*P(2,0)=7/18$

So $P(3,0)=7/18$

$P(4,3)=3/4*1/3=1/4$ [It's easy to see $P(n,n-1)=1/n$ ]

$P(4,2)=2/4*P(3,1)+2/4*P(4,1)=23/72$

$P(4,1)=3/4*P(4,2)+1/4*P(3,0)=97/288$

So $P(4,0)=97/288$

$P(5,4)=1/5$

$P(5,3)=2/5*P(5,4)+3/5*P(4,2)=163/600$

$P(5,2)=3/5*P(5,3)+2/5*P(4,1)=5359/18000$

$P(5,1)=4/5*P(5,2)+1/5*P(4,0)=54997/180000$

So $P(5,0)=54997/180000$ which is in lowest terms so $A+B=54997+180000=\boxed{234997}$

(Jeremy beat me to the punch here, my solution's no different but since I'd already made the table I thought it'd be a waste not to post it.)

Let ( $m,n)$ represent the situation that the bag contains $m$ white beans and $n$ blue beans.

Then the next draw would result in either $(m - 1, n + 1)$ , with probability $\dfrac{m}{m + n}$ , or $(m, n - 1)$ , with probability $\dfrac{n}{m + n}$ .

Thus if $P(m, n)$ denotes the probability of ending up with a single white bean from situation $(m,n)$ , then $P(m, n) = \dfrac{m}{m + n} P(m - 1, n + 1) + \dfrac{n}{m + n} P(m, n - 1)$ .

We construct a table as shown below; note we do not need a row for $m = 0$ or a column for $n = 5$ as our goal is not achievable from either of those situations.

We start with $P(1,0) = 1$ as that is our goal. In order to fill in any one of the remaining spaces, we need to use the space immediately to its left, and the one diagonally to the upper right. As an explicit example, consider the partially filled in table below:

Then the entry for $(3, 1)$ would be calculated as $P(3, 1) = \dfrac{3}{4} P(2, 2) + \dfrac{1}{4} P(3,0) = \dfrac{3}{4} \cdot \dfrac{23}{72} + \dfrac{1}{4} \cdot \dfrac{7}{18} = \dfrac{97}{288}$ .

The completed table is shown below:

The probability we need is $P(5, 0) = \dfrac{54997}{180000}$ , so our answer is $54997 + 180000 = \boxed{234997}$

The probability of white and blue beans progresses as follows:

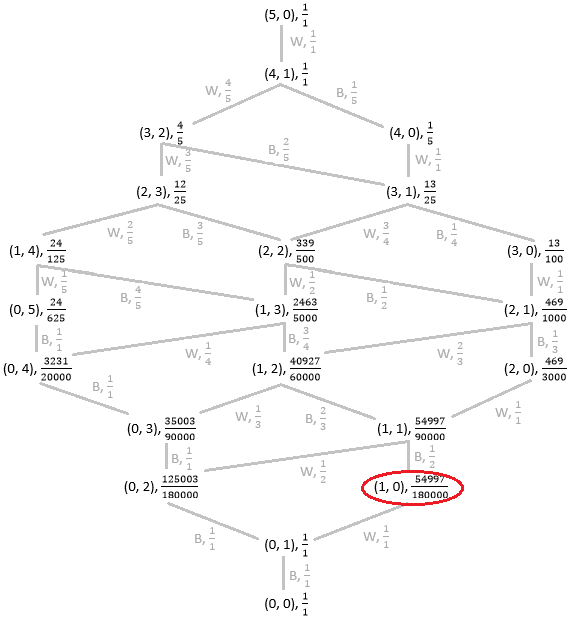
Read the tree from top to bottom, where the notation is "(white, blue), probability". So we start out with 5 white beans and 0 blue beans at a $\frac{1}{1}$ probability. Then there is a $\frac{1}{1}$ probability of picking a white bean and coloring it blue, which gives 4 white beans and 1 blue beans at a $\frac{1}{1}$ probability. Then there is a $\frac{4}{5}$ probability of picking a white bean and coloring it blue, which gives 3 white beans and 2 blue beans at a $\frac{4}{5}$ probability, and a $\frac{1}{5}$ probability of picking a blue bean and keeping it out, which gives 4 white beans and 0 blue beans at a $\frac{1}{5}$ probability. From the 3 white beans and 2 blue beans there is a $\frac{3}{5}$ probability of picking a white bean and coloring it blue, which gives 2 white beans and 3 blue beans at a $\frac{3}{5} \cdot \frac{4}{5} = \frac{12}{25}$ probability, and a $\frac{2}{5}$ probability of picking a blue bean and keeping it out, which gives 2 white beans and 2 blue beans at a $\frac{2}{5} \cdot \frac{4}{5} = \frac{8}{25}$ probability. From the 4 white beans and 0 blue beans there is a $\frac{1}{1}$ probability of picking a white bean and coloring it blue, which gives 3 white beans and 1 blue bean at a $\frac{1}{1} \cdot \frac{1}{5} = \frac{1}{5}$ probability, which can be combined with the $\frac{8}{25}$ probability of getting 3 white beans and 1 blue bean at a $\frac{8}{25} + \frac{1}{5} = \frac{13}{25}$ probability.

Branches continue to split and combine as pictured, until near the bottom (circled in red) the probability of having 1 white bean and 0 blue beans is $\frac{54977}{180000}$ , and so $A = 54977$ and $B = 180000$ , and $A + B = 54977 + 180000 = \boxed{234997}$ .

Here's the first $4$ of $14$ possible scenarios, where $1$ means a white ball has been picked and painted blue, and $0$ means a blue ball has been picked out. The probability of each action is a fraction, which all $8$ are multiplied together for a given scenario. If there is a solitrary white ball left, then exactly $8$ actions have been taken. Do the rest of the scenarios and sum up all the $14$ fractions to get the final answer. There is nothing clever at all about this solution, but this was the only way I can be sure of the final answer, which is $\frac{54997}{180000}$ .

$(1,1,1,1,0,0,0,0)$
$\dfrac { 1 }{ 1 } \cdot \dfrac { 4 }{ 5 } \cdot \dfrac { 3}{ 5 } \cdot \dfrac { 2}{ 5 } \cdot \dfrac { 4 }{ 5 } \cdot \dfrac { 3 }{ 4 } \cdot \dfrac { 2 }{ 3 } \cdot \dfrac { 1 }{ 2 }$

$(1,1,1,0,1,0,0,0)$
$\dfrac { 1 }{ 1 } \cdot \dfrac { 4 }{ 5 } \cdot \dfrac { 3 }{ 5 } \cdot \dfrac { 3 }{ 5 } \cdot \dfrac { 2 }{ 4 } \cdot \dfrac { 3 }{ 4 } \cdot \dfrac { 2 }{ 3 } \cdot \dfrac { 1 }{ 2 }$

$(1,1,1,0,0,1,0,0)$
$\dfrac { 1 }{ 1 } \cdot \dfrac { 4 }{ 5 } \cdot \dfrac { 3 }{ 5 } \cdot \dfrac { 3 }{ 5 } \cdot \dfrac { 2 }{ 4 } \cdot \dfrac { 2 }{ 3 } \cdot \dfrac { 2 }{ 3 } \cdot \dfrac { 1 }{ 2 }$

$(1,1,1,0,0,0,1,0)$
$\dfrac { 1 }{ 1 } \cdot \dfrac { 4 }{ 5 } \cdot \dfrac { 3 }{ 5 } \cdot \dfrac { 3 }{ 5 } \cdot \dfrac { 2 }{ 4 } \cdot \dfrac { 1 }{ 3 } \cdot \dfrac { 1 }{ 1 } \cdot \dfrac { 1 }{ 2 }$

etc