Beastie problem!
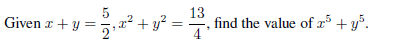 The answer to this question can be expressed as
b
a
. Calculate the sum of
a
+
b
The answer to this question can be expressed as
b
a
. Calculate the sum of
a
+
b
The answer is 307.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
a^3 + b^3 = (a + b)^3 − 3ab(a + b) put here a=x^2 and b=y^2... then we solve this we find x^5+y^5= 793/64 then ans will be 857... what's wrong with this.?
Log in to reply
Found it! If a=x^2, then a^3 will equal (x^2)^3 = x^6. The question asks you to find x^5, and not x^6.
Simply I found that.
X=3/2
y=2/2
I found (x+y)^2=(5/2)^2 x^2+2xy +y^2 =25/4 x^2+y^2+2xy=25/4 13/4+2xy=25/4 2xy=25/4-13/4 2xy=3 xy=3/2 NOW x+y=5/2-(1) xy=3/2-(2) By solving this system of simultaneous equations,I got x=1,y=3/2 plugging these values in i got 243/32 so 243+32=307......YAYYYY!!!
did same way!
e = 2
x = e c , y = e d
c + d = 5
c 2 + d 2 = 1 3
c = 3 , d = 2
c 5 + d 5 = 3 5 + 2 5 = 2 4 3 + 3 2 = 2 7 5
b = e 5 = 2 5 = 3 2
a + b = 2 7 5 + 3 2 = 3 0 7
Add 2 x y to both sides of x 2 + y 2 = 4 1 3 :
x 2 + 2 x y + y 2 = 4 1 3 + 2 x y
( x + y ) 2 − 4 1 3 = 2 x y
( 2 5 ) 2 − 4 1 3 = 2 x y
x y = 2 3
Now, from ( x + y ) 5 = x 5 + 5 x 4 y + 1 0 x 3 y 2 + 1 0 x 2 y 3 + 5 x y 4 + y 5 obtain x 5 + y 5 :
x 5 + y 5 = ( x + y ) 5 − 5 x y ( x 3 + y 3 ) − 1 0 ( x y ) 2 ( x + y )
x 5 + y 5 = ( x + y ) 5 − 5 x y ( x + y ) ( x 2 + y 2 − x y ) − 1 0 ( x y ) 2 ( x + y )
x 5 + y 5 = ( 2 5 ) 5 − 5 ( 2 3 ) ( 2 5 ) ( 4 1 3 − 2 3 ) − 1 0 ( 2 3 ) 2 ( 2 5 )
x 5 + y 5 = 3 2 2 7 5
Hence, a = 2 7 5 , b = 3 2 and a + b = 3 0 7 .
x+y=5/2
(x+y)²=x²+y²+2xy
25/4=13/4+2xy
xy=3/2
So x & y are 2 numbers whose sum=5/2 and product=3/2
So they will satisfy the equation ∅²-S∅+P=0 which is quadratic in ∅
∅²-(5/2)∅+(3/2)=0
2∅²-5∅+3=0
∅=1,3/2=(x,y) or (y,x)
x 5 + y 5 = 1 + ( 2 4 3 / 3 2 )
=275/32≈a/b
a+b=275+32=307
x+y =5/2 .........(1)
x^2+y^2 = 13/4 ............(2)
from (1) x= 5/2 -y ...............(3)
put in (2) => (5/2-y)^2 +y^2 =13/4
25/4 +y^2 -5y + y^2 =13/4
=> 2y^2 -5y = 13/4 -25/4
=>2y^2-5y=-3
by solving this quadratic eq. we get roots y= 1 & 3/2 => y^5=243/32 &1
by putting the values of y in (3) we have x= 3/2 &1 => x^5 = 243/32 &1
=> x^5+y^5= 243/32+1= 275/32 =a/b
hence a+b = 307
(x+y)^2 = x^2+2xy+y^2 = 25/4 13/4+2xy = 25/4 xy = 3/2
x^3+y^3 = (x+y)(x^2+y^2-xy) = 5/2*(13/4-3/2) = 35/8
x^5+y^5 = (x^3+y^3)(x^2+y^2) - (xy)^2(x+y) = (35/8)(13/4) - (9/4)(5/2) = 275/32 = a/b so a+b =307
Am I the only one that tried to solve a + b = b a at first?
ooh sorry but i did not not think it was going to be confusing?
Log in to reply
Lol no problem :D.I just thought that until I saw the image :D
From ( x + y ) 2 = x 2 + 2 x y + y 2 ,
⇒ ( 2 5 ) 2 = 4 1 3 + 2 x y
⇒ 2 x y = 4 2 5 − 4 1 3 = 4 1 2 = 3
Now, x ( x + y ) = ( x ) 2 5
⇒ 2 x 2 + 2 x y = 5 x
2 x 2 + 3 = 5 x
2 x 2 − 5 x + 3 = 0
( 2 x − 3 ) ( x − 1 ) = 0
⇒ x = 2 3 , 1 ⇒ y = 2 3 , 1
Note that x and y are interchangeable. ( x , y ) = ( 2 3 , 1 ) , ( 1 , 2 3 ) .
Therefore,
x 5 + y 5 = 1 5 + ( 2 3 ) 5 = 1 + 3 2 2 4 3 = 3 2 2 7 5 = b a
⇒ a + b = 3 0 7