Beautiful Area Between The Lines And The Curve
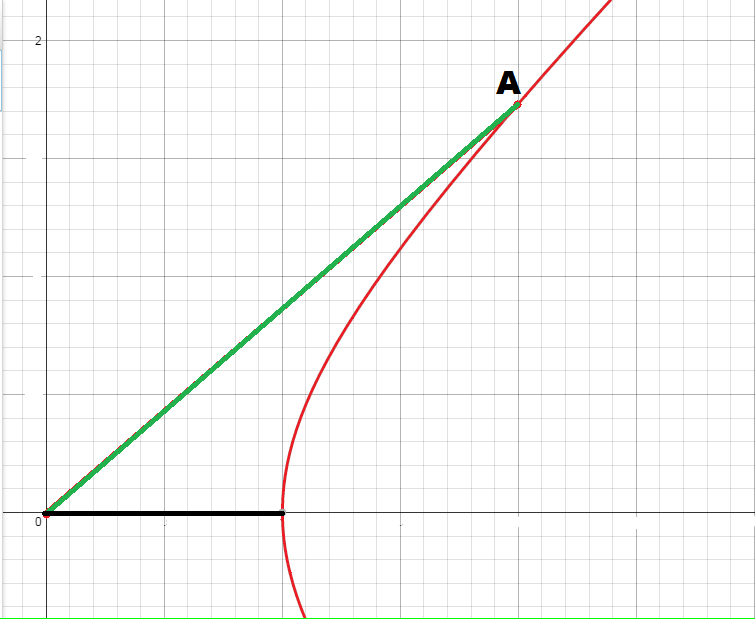
In the above graph, the red curve is a part of the curve (mostly in the first quadrant). A point lies on this red curve and is connected to the origin by the green line segment.
If the -coordinate of point equals , find the area bounded by the red curve, green line segment and the black -axis in the first quadrant.
The answer is 1008.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let any point on the hyperbola be ( x , x 2 − 1 ) .
The area under the line drawn from origin to the point is
Δ 1 = 2 1 × x × y = 2 x x 2 − 1
The area under the hyperbola is given by,
Δ 2 = ∫ 1 x t 2 − 1 d t
It can be derived very easily integrating by parts,
∫ t 2 − a 2 d t = 2 t t 2 − a 2 − a 2 ln ( t + t 2 − a 2 )
Putting a=1 and substituting the limits,
∴ Δ 2 = 2 x x 2 − 1 − ln ( x + x 2 − 1 )
Required area is,
Δ r e q = Δ 1 − Δ 2
∴ Δ r e q = 2 ln ( x + x 2 − 1 )
For the given question, substitute x = 2 e 2 0 1 6 + e − 2 0 1 6 , and Δ r e q comes out to be 1008.