Beautiful Integral

Calculus Level 3

∫ a b ( x − a ) ( b − x ) d x = ? \large\int\limits_{a}^{b}\sqrt{(x-a)(b-x)}\,\mathrm dx~=~?

Assume that b > a b>a .

( a − b ) 2 (a-b)^{2} π ( a + b ) 2 8 \frac{\pi (a+b)^{2}}{8} π ( a − b ) 2 8 \frac{\pi (a-b)^{2}}{8} ( a + b ) 2 (a+b)^{2}

View wiki
Jessica Wang by Jessica Wang , 22, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

7 solutions

Jessica Wang
Oct 28, 2015

43 Helpful 0 Interesting 0 Brilliant 0 Confused

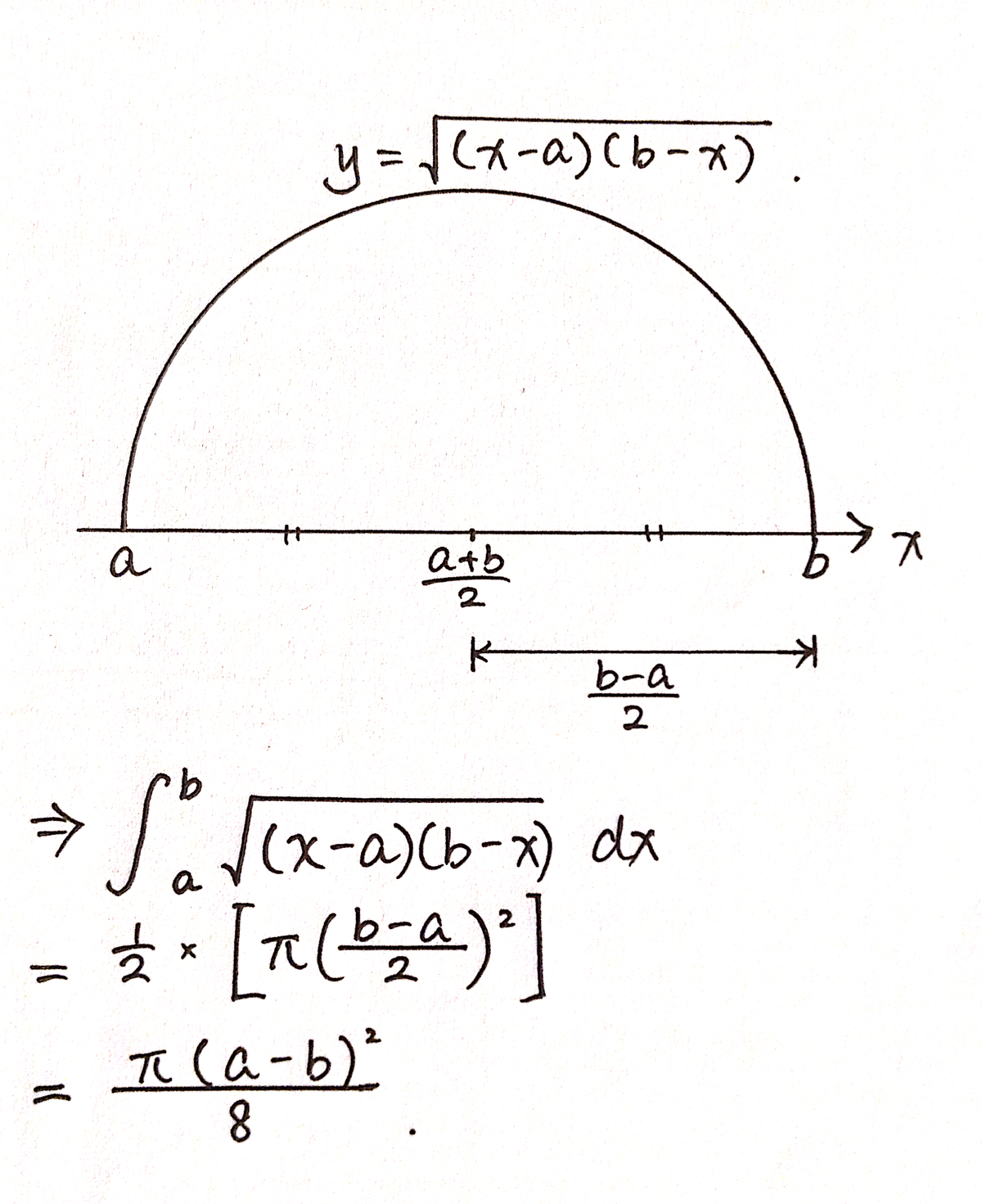
That's one of the beautiful solution i seen on brilliant.
For those who didn't get how you made that semicircle...
y = ( x − a ) ( b − x ) y = \sqrt{(x - a)(b - x)}
Squaring both sides,

⇒ y 2 = x b − x 2 − a b + a x \Rightarrow y^2 = xb - x^2 - ab + ax .
⇒ x 2 + y 2 − ( a + b ) x + a b = 0 \Rightarrow x^2 + y^2 - (a+b)x + ab= 0 .
Above equation, is an equation of cicle with center at ( a + b 2 , 0 ) \left(\dfrac{a + b}{2},0\right) and the radius b − a 2 \dfrac{b - a}{2} (from diagram) ,but y can't be negative. hence, y = ( x − a ) ( b − x ) y = \sqrt{(x - a)(b - x)} is an equation of half circle lying above x - axis.

Akhil Bansal - 5 years, 7 months ago

Nice geometrical approach @Jessica Wang !!

A Former Brilliant Member - 5 years, 7 months ago

Log in to reply

Thank you Abhi @Abhineet Nayyar :)

Jessica Wang - 5 years, 7 months ago

Nice solution.

Kushal Patankar - 5 years, 7 months ago

Log in to reply

The way I solved it was by substituting x = a ( s i n x ) 2 + b ( c o s x ) 2 a(sinx)^2 + b( cosx)^2 But, this method is simply more elegant and beautiful!

A Former Brilliant Member - 5 years, 7 months ago

I noticed the symmetry of the integrand about x = 1 2 ( a + b ) x=\frac 12(a+b) while solving the problem but didn't think that it was gonna be a nice geometric figure (semicircle in this case). Ended up bashing the integral with basic properties of definite integrals and some known closed forms. Nice problem.

Prasun Biswas - 5 years, 7 months ago

Log in to reply

I found the same. I knew that there was symmetry but I didn't realize I was dealing with a semicircle until I got to the step of evaluating

( b − a ) 2 4 ∫ − 1 1 1 − u 2 d u . \dfrac{(b - a)^{2}}{4} \displaystyle\int_{-1}^{1} \sqrt{1 - u^{2}} du.

Nice problem and an elegant solution, @Jessica Wang . :)

Brian Charlesworth - 5 years, 7 months ago

Log in to reply

Thank you sir :) @Brian Charlesworth

Jessica Wang - 5 years, 7 months ago

wat ıntegrate formula

Soner Karaca - 5 years, 7 months ago

Nice picture~<3

展豪 張 - 5 years, 7 months ago
Michael Mendrin
Oct 29, 2015

I hate to be a party pooper, but the correct answer is actually

1 8 π ( b − a ) ( b − a ) 2 \dfrac { 1 }{ 8 } \pi \left( b-a \right) \sqrt { { \left( b-a \right) }^{ 2 } }

Otherwise, if a > b a>b , the sign would be wrong. Work it out. The hangup is that the limits of the definite integral can actually result in a negative value if a > b a>b , but if the limits were to be reversed, i.e, integrate from b b to a a if a > b a>b , then it would return a positive value.

This problem, as posted, should have included the condition that b > a b>a .

5 Helpful 0 Interesting 0 Brilliant 0 Confused

@Michael Mendrin Thank you very much for pointing this out -- I have edited the problem!

Jessica Wang - 5 years, 7 months ago
Will Jain
Nov 1, 2015

That's a really beautiful Sol by Jessica Wang

2 Helpful 1 Interesting 0 Brilliant 0 Confused
Arjen Vreugdenhil
Oct 28, 2015

A slightly different approach: rewrite the expression under the square root by "completing the square": ( x − a ) ( b − x ) = − ( x − c ) 2 + d . (x-a)(b-x) = -(x-c)^2 + d. Since the linear term is − ( a + b ) x -(a+b)x , we find c = 1 2 ( a + b ) c = \tfrac12(a+b) ; and because the constant term is − a b -ab , d = c 2 − a b = ( 1 2 ( a + b ) ) 2 − a b = ( 1 2 ( a − b ) ) 2 = : r 2 . d = c^2-ab = (\tfrac12(a+b))^2 - ab = (\tfrac12(a-b))^2 =: r^2. Thus we find ( x − a ) ( b − x ) = r 2 − ( x − c ) 2 , \sqrt{(x-a)(b-x)} = \sqrt{r^2-(x-c)^2}, which we recognize the equation for a circle with center ( c , 0 ) (c,0) and radius r r .

It makes sense that the center of the circle is precisely the average of a a and b b , and that the radius is precisely half of the distance between a a and b b ... The line from ( a , 0 ) (a,0) to ( b , 0 ) (b,0) is a diameter of the circle.

The integral gives, naturally, the area of a semicircle: A = 1 2 π r 2 = 1 8 ( a − b ) 2 . A = \tfrac12 \pi r^2 = \tfrac18 (a-b)^2.

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Kevin Yang
Dec 28, 2018

According to Wolframalpha it's 1 8 π ( a − b ) 2 \frac{1}{8}\pi(a-b)^2

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Ramez Hindi
Nov 4, 2015

my tr y

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Righved K
Oct 29, 2015

did it by beta function..done with ease

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I am not very familiar with using special functions. Would you mind posting your solution so I can learn? If it is too much trouble, then it is fine.

Varun Gudibanda - 5 years, 7 months ago

Log in to reply

Sorry john for looking late but please tell me how to share the solution with you,I have a snap of the solution

Righved K - 5 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...