Beautiful triangle problem
 interesting geometry puzzle
interesting geometry puzzle
As shown above, in a triangle two lines are drawn such that three angles (marked blue) are equal. If the area of the two small triangles are 4 and 9, find the area of yellow quadrilateral.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
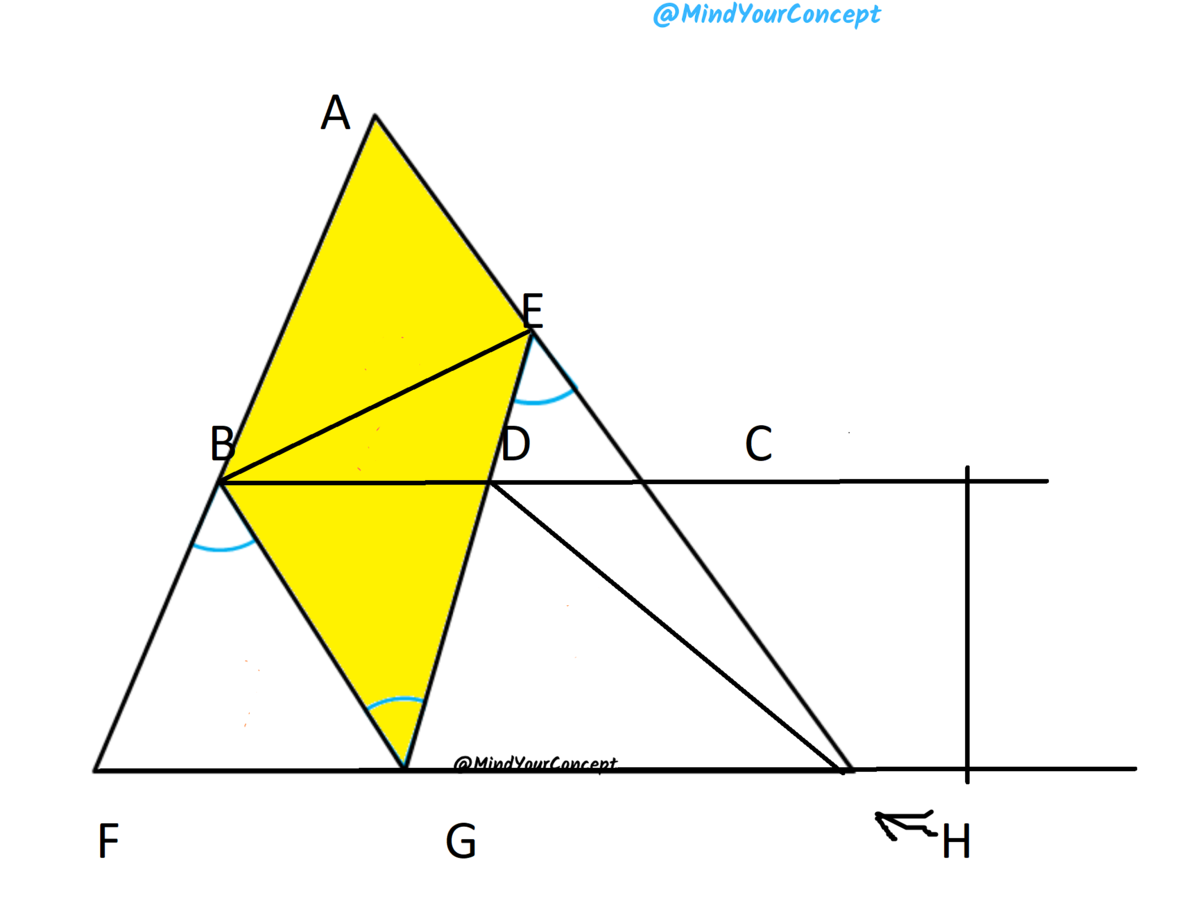
let [ B D ] ∣ ∣ [ F H ]
∠ F B G = ∠ B G D Hence [ B F ] ∣ ∣ [ D G ]
so ∠ B F G = ∠ E G H , ∠ B G F = ∠ E H G hence B F G and E G H are similar and [ A E ] ∣ ∣ [ B G ]
their areas ratio is 9 4 so their similarity ratio is 3 2
let ∣ F G ∣ = 2 a then ∣ G H ∣ = 3 a
heights of B F G and D G H are equal so their area ratio will be 3 2
area of B F G is 4 then area of D G H is 6 and area of E D H is 3 . So ∣ E D ∣ ∣ D G ∣ = 3 6 = 2 = a r ( E D B ) a r ( B D G )
B D G F is a parallelogram hence a r ( B D G ) = a r ( B F G ) = 4 so area of E B D is 2
again A B G E is a parallelogram Hence a r ( A B E ) = a r ( B E G ) = 4 + 2 = 6
area of A B G E is sum of the areas of A B E and B E G ⇒ 6 + 6 = 1 2
Note:sorry i couldnt draw DH good
Let the vertices of the whole triangle be A , B , C , the vertex of the yellow quadrilateral on the side B C be D , on the side C A be E , and on the side A B be F . Let ∣ B C ∣ = a , ∣ C A ∣ = b , ∣ A B ∣ = c . Since D F and C A are parallel, therefore, let ∣ B D ∣ = p a , ∣ D C ∣ = q a , ∣ B F ∣ = p c , ∣ F A ∣ = q c . Since D E and B A are parallel, therefore ∣ C E ∣ = q b , ∣ E A ∣ = p b . Area of △ B F D = 4 = 2 1 p a × p c × sin B , where B = ∠ A B C . So p 2 △ = 4 , where △ is the area of △ A B C = 2 1 a c sin B = 2 1 b c sin A = 2 1 a b sin C . ( A = ∠ B A C , C = ∠ A C B ). Therefore △ = p 2 4 . Area of △ D C E = 9 = 2 1 q a × q b × sin C = q 2 △ . So △ = q 2 9 . From this we get q = 2 3 p . Hence, area of the quadrilateral A E D F is p b × q c × sin C = 2 p q △ = 3 p 2 △ = 3 × 4 = 1 2
Let's label the figure as above. We note that external angle ∠ D E C = ∠ B D E + ∠ D B E . Since ∠ D E C = ∠ D E F + ∠ F E C , and ∠ D E F = ∠ B D E ⟹ ∠ F E C = ∠ D B E . Therefore △ D B E and △ F E C are similar. We also note that △ A B C is also similar to the two small triangle. Since the area of similar triangles are proportional to the square of their linear dimension. Then, if △ D B E has a base length of 2 a , △ F E C has a base length of 3 a . Therefore, the base length of △ A B C is 5 a and the area [ A B C ] = 2 5 , and the area of the yellow quadrilateral [ A D E F ] = [ A B C ] − [ D B E ] − [ F E C ] = 2 5 − 4 − 9 = 1 2 .