Beautifully charged bead

Electricity and Magnetism Level 5

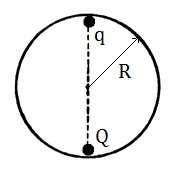A little charged bead is inside a fixed and uncharged hollow sphere of radius $R$ made of insulating material. The mass of bead is m and charge is $q$ . A charge $Q$ when kept at bottom of the hollow sphere, the bead is in equillibrium at the vertex of the sphere. If the bead is in stable equillibrium then $Q \geq$

Assume $k$ is an electrostatic constant.

\dfrac{mgR^2}{kq}

\dfrac{4mgR^2}{kq}

\dfrac{mgR^2}{2kq}

\dfrac{8mgR^2}{kq}

1 solution

Ťånåy Nårshånå
Jul 3, 2015

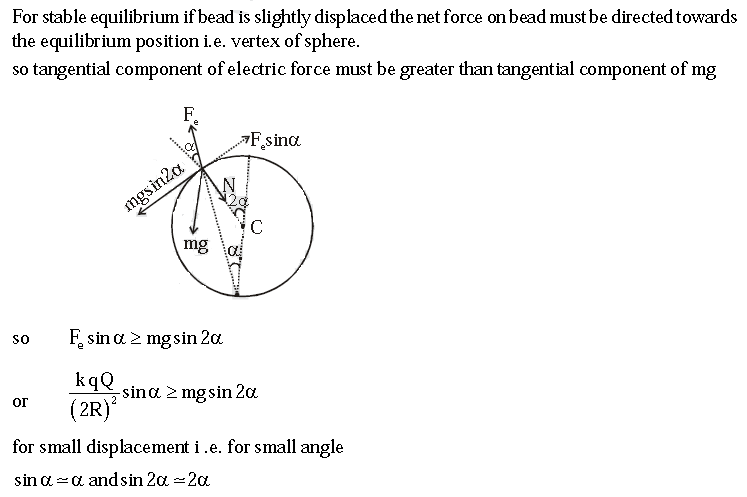
If change in potential energy is positive, then also the position is stable equilibrium position so using this we get a factor 4 rather than 8.

@Spandan Senapati please help.

Harsh Shrivastava - 4 years, 1 month ago

Lets displace by an angle $\alpha$ .Stick to the horizontal passing through centre as the reference for gravitational potential energy.So $U(\alpha)=(kqQ/2R)sec\alpha /2+mgRcos\alpha$ .Now differentiate wrt $\alpha$ and use approximation .You will get $Q>=8mgR^2/kq$

Spandan Senapati - 4 years, 1 month ago

Thanks bro, I did a bad mistake, took angle subtended at arc also to be alpha, I was sleepy at morning :P

Harsh Shrivastava - 4 years, 1 month ago

Yes $d/dx(dU/dx)>0$ .I too took the same that displacements are in vertical direction rather its along the sphere itself.So Write the potential energy and see you will get it.

Spandan Senapati - 4 years, 1 month ago

Beautifully charged bead

1 solution

0 pending reports