Beauty inside a Square : 2
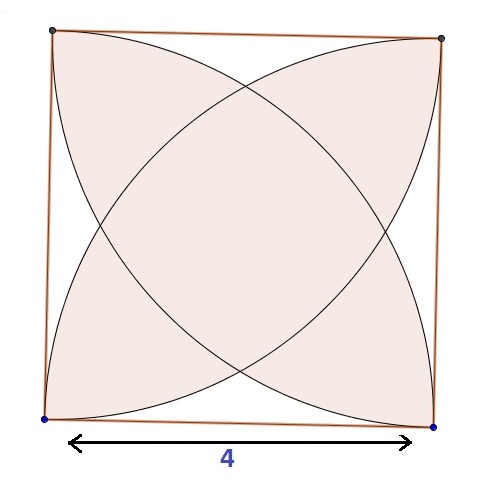 This is a square with side length
4
. Taking
4
as radius an arc is drawn inside the square from each vertex. The
4
arcs create a diagram as shown in the picture.
This is a square with side length
4
. Taking
4
as radius an arc is drawn inside the square from each vertex. The
4
arcs create a diagram as shown in the picture.
Find the area of the shaded part.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Thanks for adding a solution!
Note: For markdown, you have to link to the image file (which has an extension of .jpg, .png, etc) instead of the entire webpage. I've edited your solution to display the image.
Log in to reply
Thanks for fixing it!
I think the images are still not visible in the solution. Is anyone else facing this issue ?
Log in to reply
With spaces removed,
! [image] (link)
I've edited your comment so you can see how to attach a picture.
area = 16 - 8*integral {4-(16-x^2)^0.5} where x varies from 0 to 2
= ans.
how to add picture in a solution ?
Good solution
brilliant!
What a good solution. But i can't understand the first picture explains. Formula area for find equilateral triangle and the right pink shaded part(the degree too). Can someone explain?
Log in to reply
If a is the side of an equilateral triangle, then it's area is 4 3 a 2
And The area of circle is π r 2 which has an interior angle of 3 6 0 ∘ .
1 2 3 6 0 ∘ = 3 0 ∘ .
So, the area of a single pink part is 1 2 π r 2
thanks
Really nice problem....
You r truely a brilliant...
interesting
excellent
thanks for this problem but i did'nt get how the triangle formed is an equilateral. I cant prove it XD
Log in to reply
Thanks for the fantastic solution.
\boxed{14}
 enter image description here
enter image description here
Consider the Region HEFG, the Area of HEFG can be expressed as = A A B C D − 4 × A D G F C D = A A B C D − 4 × ( A A E F C D A − ( A A E F D A + A D F G D ) ) = A A B C D − 4 × ( A A E F C D A − ( A A E F D A + ( A A F G D A − A A F D ) ) ) = r 2 − 4 ( 4 π r 2 − ( 6 π r 2 + ( 6 π r 2 − 4 3 r 2 ) ) ) r 2 − 4 ( 4 π r 2 − 3 π r 2 + 4 3 r 2 ) = r 2 − 4 ( − 1 2 π r 2 + 4 3 r 2 ) = r 2 + 3 π r 2 − 3 r 2
So
A_{HEFG} = r^2 + \frac{\pi r^2}{3}-\sqrt{3}r^2\tag1
Now,
A A E B F C G D A = 4 × A A E F C A − A H E F G = 4 × ( A A E F C D A − A A C D A ) − A H E F G = 4 × ( 4 π r 2 − 2 r 2 ) − A H E F G = 4 × ( 4 π r 2 − 2 r 2 ) − A H E F G = 4 × ( 4 π r 2 − 2 r 2 ) − A H E F G = π r 2 − 2 r 2 − A H E F G
= π r 2 − 2 r 2 − r 2 − 3 π r 2 + 3 r 2 = ( 3 + 3 2 π − 3 ) r 2
8*pi-16
Log in to reply
your answer is wrong because you have counted the middle part twice
Your answer is also wrong because you treated arcs as straight lines. You cant count the area of DGFC as a common geometric shape. it's bend forming an arc
My solution was exactly the same as Fahim's. This was one of my favourite geometry problems from high school.
This can be solved with analytic geometry and calculus as follows. If we consider the box to be [0, 4]x[0,4] in R^2, the shaded area is the area of the total square (which is 4x4 = 16) minus 8 times the area bounded by y = 4 and y = (16-x^2)^.5 between x = 0 and x = 2 (by symmetry). The latter area can be computed as the integral from x = 0 to x = 2 of f(x) = 4-(16-x^2)^.5. This integral can be computed via the trigonometric substitution x = 4*sin(theta). Simplifying yields the desired answer.
Find Area Shaded into the square with side L = r = 4
If we denote with:
A , B , C , D the vertices of the square clockwise from bottom left to top left;
E , F , G , H , points of intersections between the circles clockwise from top center to right center;
E 1 , F 1 , G 1 , H 1 , the projections of E , F , G , H , on the closest side of
the square, we have:
A s h = A s − 8 A ( E 1 D E ) ;
we denote:
A s h :=Area Shaded;
A s := Area Square = 4 2 = 1 6 ;
E 1 D E : the surface between perpendicular segments E 1 D , E E 1 and D E ⌢
we have:
A ( E 1 D E ) = A ( A G 1 E 1 D ) − A ( A G 1 E D ) − A ( A G 1 E ) ;
∠ D A E = 6 π , because ∣ A E ∣ = ∣ B E ∣ = ∣ A B ∣ = 4 , and △ ( A B E ) is equilater, so ∠ B A E = 3 π ,
and ∠ D A E = θ 0 = 2 π − 3 π = 6 π ; thus:
A ( A G 1 E D ) = 2 1 θ 0 r 2 = 2 1 6 π × 1 6 = 3 4 π
A ( A G 1 E 1 D ) = 2 × 4 = 8 ;
A ( A G 1 E ) = 2 1 ∣ A G 1 ∣ ∣ G 1 E ∣ = 2 1 × 2 × 4 × sin ( 3 π ) = 4 2 3 = 2 3 ;
A ( E 1 D E ) = 8 − 2 3 − 3 4 π ;
A s h = 1 6 − 8 ( 8 − 2 3 − 3 4 π ) ;
A s h = 1 6 3 + 3 2 3 π − 4 8 = 1 3 . 2 2 3 1 3 4 5 6 . . .
13 square unit or 13.20 square unit
area =integral {4-sqrt(16-x^2)} 0 to 2 = 16-4 area 2
In the 1st picture
The area of the equilateral triangle is 4 4 2 3 = 4 3
The right pink shaded part is a part of a circle. As its internal angle is 3 0 ∘ , its area is 1 2 π r 2 = 1 2 4 2 π = 3 4 π
So, total area of pink shaded parts = 2 × 3 4 π = 3 8 π
Hence the area of the white part = ( 1 6 − 4 3 − 3 8 π )
In the 2nd picture
Total white part = 4 ( 1 6 − 4 3 − 3 8 π )
Hence, Area of shaded part = 1 6 − 4 ( 1 6 − 4 3 − 3 8 π )
= 1 6 3 + 3 3 2 π − 4 8