Beauty inside a Square
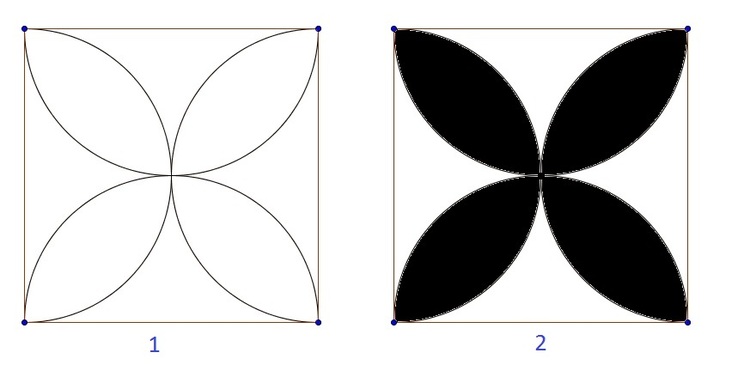 This is a square with side length
4
. Semi circles are drawn on each side of the square (as shown in the picture). Find the area of the shaded (black) part.
This is a square with side length
4
. Semi circles are drawn on each side of the square (as shown in the picture). Find the area of the shaded (black) part.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
27 solutions
I also did it in the same way!
the area of the shaded part = the area of the semi circle * 4 - the area of square = 2 2 π − 4 2 = 8 π − 1 6
Log in to reply
I think your solution is incorrect but you got the answer right. You missed this:
2(πr^2 ) - s^2
2(π2^2 )- 4^2
8π-16
2 power 2 +2
the idea is right anyway
VERY GOOD YOU ARE CORRECT
Let's think in a different way that is unusual but it works well to find the answer. 1st eq : (4 shaded+ 4 unshaded= 16) which is the area of the square, 2nd eq ( 2 shaded+ 1 unshaded =2 Pi) , which is the area of the semi circle. by solving the two equation altogether we find that "2 unshaded= 16- 4 Pi". By using the last value of the unshaded in any of the above equation Like 1st eq : (4 shaded+ 4 unshaded = 16 ). you will get the correct answer which is 4 shaded = 8 pi - 16.
Log in to reply
IT IS VERY NEER TO MY ANSWER
Log in to reply
انا مش عارف اعبر بس انت اكيد هتفهمي انت عربي (انا قلت لو هنفرض الجزء اللي شبه المثلث ده (س والجزء اللي شبه اللوزه (ص والمساحه المطلوبه 4ص هنجيب معادلتين علشان في مجهولين المعادله الاولي نصف مساحه المربع =2س+2ص المعادله التانيه نصف مساحه الدايره=2ص+س ونحلهم مع بعض نجيب ص المطلوب 4ص
I just thought that answer should be easily divisible by 4 and got it right by chance
Area of quadrant= 1/4 * pi *2^2= pi..Area of triangle = 1/2 *2 * 2 = 2.... Area of segment = pi - 2... Total area = 8 ( pi - 2) = 8pi-16
I remember my Solid Mensuration days.
me too!!!!
yes i have also done like this
nice solution
I did it in the same way
area of triangle made of half the side of square which is half of the area of one quarter of the square is 1/2 1/2 1/2= 1/8 Area of the quarter of the circle with radius of 1/2 is square side is pi*(1/2)sq /4 =pi16/ so the are of quarter of a circle is minus 1/8 of the square is pi/16 - 1/8 which is (pi-2)/16. multiplying it by 8 for 8 triangles is (pi -2)/2 the only answer which is multiple of (pi-2)/2 is 8pi -16
exactly the same way as above
evn i did in the same way..
me too did it in the same way
yes, i did it in the same way! :)
sme way bt calculated wrongly...
I ALSO DID THE SAME WAY!
got the same answer. but did it in some other way.
i solved it in the same way !!!
We can also assume the shaded region being divided into 4. Then area of one strip can be calculated then multiplied by 4. Result will be same i.e. 8pi-16
solid mensuration by kern and bland, 2nd edition, pg. 43, problem no. 15..
THE SHADED AREA EQUAL TO 8 (ΠR^2 m/360 -the corresponding triangle)so is 8 (π 2^2/4 -2*2/2)
I HAVE AVERY DIFFERENCE ANSWER IT IS SO EASY BUT I CANNOT UPLOAD MY PHOTO
that's the exact same thing I did, but instead of 2 pi+ 2 pi I did 4 pi.
Woah !!! 7 3 upvotes. That's a record I believe.
See the picture below.
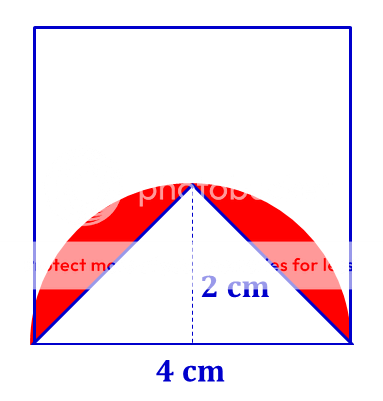 Flower in Circle
Flower in Circle
Area of shaded (red) part is A = [ semicircle ] − [ triangle ] = 2 1 π ( 2 ) 2 − 2 1 ⋅ 4 ⋅ 2 = 2 π − 4 Area of shaded ( black ) part is A = 4 ( 2 π − 4 ) = 8 π − 1 6
First of all, we add 4 semicircles with r = 2. We see that the petals are counted twice, and the non-petals are counted once.
Then we subtract by the entire square. The petals are now subtracted so we count them only one. And the non-petals are all gone too.
The area = 4 ( 2 1 π × 2 2 ) − 4 2 = 8 π − 1 6 .
This technique's called inclusion-exclusion. Can be used almost every problem when I do these stuffs. You don't have to find the area of specific part like petals and multiply by number of pieces. This one's also able to do some problems that other techniques can't.
i like this one the best!! Its an elegant solution.
This one is the best.
Exactly the same as u did
thats the way i did
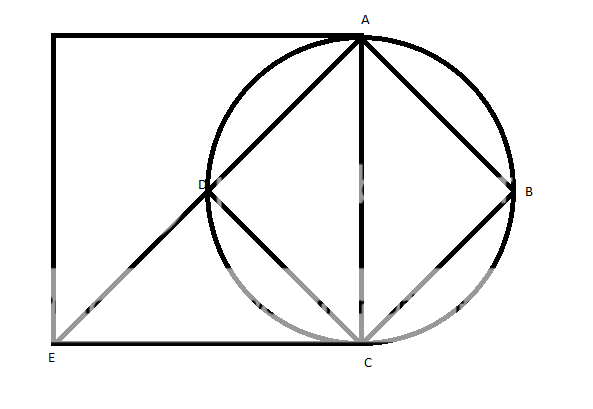 Solution
Solution
As you can see in the picture, we have:
A E = 3 2 A D = 2 3 2 S A B C D = 8
call O is outer circle that wrap around ABCD
S O = 4 π
So the remaining area is equal to
S O − S A B C D = 4 π − 8
The area of haft petal is
4 4 π − 8 = π − 2
Finally the area 4 petal is: ( π − 2 ) ∗ 8 = 8 π − 1 6
Area of two semi circle drawn from two opposite side =one full circle of dia 4=4π Rest of the two same sizes area =4^2-4π=16-4π. So rest of the 4 same sizes Area=2*(16-4π)=32-8π So finally the shaded Area=Area of Square - Area of the rest 4 same sizes Area=16-(32-8π)=8π-16
the required area is the square's area subtracted from the area of four semicircles. 8pi - 16
Start by finding the area of half of one of the black "petals." This can be achieved by taking half of one of the semicircles (a quarter circle) and subtracting out a triangle. The area of a full circle would be 4 π so the area of a quarter circle is π . The triangle is an isosceles right triangle with leg length 2 , so its area is 2 . Subtracting the triangle from the quarter circle will give you the area of half of one of the "petals." This is equal to π − 2 , so the area of a full petal is 2 π − 4 . There are 4 petals. so the total area of the black "flower" is 8 π − 1 6
Well explained.
this was my solution :)
The entire area inside the square is covered by four semicircles( including the area which is shaded and covered twice) , four semicircles are equal to two circle. radius of the circle is 2 ( side of square is 4). Are of two circles with radius to 2 is 8* PIE. As the four semicircles cover the whole area of the square + the area of intersection. So the area of intersection i.e shaded part is 8 PIE - (area of square) = 8 PIE -16.
just take a litle part of this cicle. then power 8. so the answer is 8phi-16
Let the area of the shaded portion =4x, (4 eqal segments),
Area of the semi circle each is = s, and
the area other than the shaded portions in the semi circle = y,
As we can know from the picture, 2x=s-y,
Hence 4x= 2s-2y, ...(a)
Also 4x=(area of the squre)-4y, = 16-4y, ...(b),
Hence (a)=(b),
i.e. 2s-2y = 4^2 -4y,
2(2#)-2y = 16-4y,
Hence on solving we can get y = 8-2#,
Hence putting on (a) we get 4x = 2(2#) - 2(8 - 2#),
= (8# - 16),
= The required answer.
Take a part of shaded portion as Y. Take a part of unshaded portion as X. Taking whole square into account, 4X + 4Y=16 (Area of square=16) X+Y=4.....Take it as equation1.. Taking a semi circle into account, 2Y+X=2Pi (Area of semicircle=2Pi) Take it as equation2.. Solve 1 and 2... Y=2Pi-4, 4Y=8Pi-16......
Area of shaded region = (sum of areas of 4 semicircles) - area of square = 9.1327 ≈ 8 π -16
Calculate area of 1 semi-circle and multiply it by 4. Now you get the area of square + area of shaded region. Therefore, subtract area of square from it to get area of shaded region.
total area of square =16; area occupied by two semi circles =4 pi; two parts of unshaded area =16-4 pi;total unshaded area =2(16-4 pi); shaded area =16-unshaded area;16-2(16-4 pi);8*pi-16
4 half circle area 8pi area of black shaded area =area of squre-8pi=16-8pi
8pi -16
area of 4 semicircles -area of square
There are 4 semi circles,i.e 2 circles.The area of one semi circle=pi 2 2/2,,,=2pi. If we consider,2 semi circle,which lies opposite,the total area of the 2 semi circle is 4pi.So the area of the rest part =16-4π.And there is 2 semi circle and remaining part.The area of the remaining =16-4π.So the area of the shaded part=16-(the area of square)32-8π 16-(32-8π),,=16-32+8π= 8π-16
Simply: First calculate the area of whole square i.e. 4 x 4 = 16 Then calculate the area of one whole circle (note: there are two full circles inside) i.e. 4π Now subtracting 4π from 16 gives = 16-4π 16-4π/2 = 8-2π which is not-shaded-upper-and-lower part each inside the square Area of a semi-circle i.e. π4/2 = 2π Now subtract 8-2π from 2π i.e. 4π-8 4π-8/2 = 2π-4 (each of the above shaded parts) Hence, 4* (2π-4) = 8π-16.
area of the small triangle=(1/2) 2 2=2 area of one fourth of circle=1/4(pi 4)=pi area of one such shaded portion=2 (pi-2) reqd area=4 2 (pi-2) =8pi -16
Sides of square=4cm radius of semicircle=sides of square/2 = 2 cm
since there a four semicircles area of shaded region = area of 4 semicircle-area of square =4 πr^2 - 4 4 -------- 2 =2 π 4 - 16 =8π-16
area of square=4*4=16 now a=one of the intersected small region like banana b=one of the other region like Eiffel tower in paris. then area of semi circle=2 pi we can get 2 equations 4a+4b=16 and 2a+b=2 pi then solve ,gives a=(8 pi-16)/4 required area=4 a=8 pi-16 hence the answer.
there are 4 black parts and 4 white parts. now,
1 black part = x
1 white part = y
now, area of the square = 4 * (x) + 4 * (y) .
16 = 4x + 4y........eq.(1)
also,
area of the semi circle = 2 * (x) + y
0.5 * (pi) * 4 = 2 * (x) + y
2(pi) = 2x +y..........eq. (2)
solving these 2 equations , we get x =2(pi) - 4
hence, area of black part is 4 * (x) = 8 (pi) - 16
Taking a quarter of the big square we now have a 2 by 2 square. The shaded area is 8 segments of a circle. To get the area of a segment of a circle is area of a sector minus the area of the triangle.
Area of a sector is:
(r^2/2)∅ , where ∅ is equal to π/2 in radian which gives
(r^2/2)*(π/2)=(πr^2)/4
Area of a triangle is:
bh/2 = (2*2)/2 = 2
Area of a segment is:
(πr^2/4)-2
Multiplying this into 8 we get:
2πr^2-16
Putting 2 as r we get:
8π-16
1st vve find the area of semicircle vvith radius is 2, area of shaded region=sum of area of 4 semicircle - area of square
The little dark (1 of total 4) area is A=2 (1/2) r^2 (theta(radian) - sin (theta)) , theta = 90, r=2 So total dark area will be 4 A
Reduce the problem into the smaller square of 2x2. Integrate y=4 - x^2 from 0 to 2 ( formula for the circle is x^2+y^2=4 for the semi circle inside the 2x2 square) The result is pi. This area minus the equilateral triangle of 2x2 gives you pi-2. Multiply by 2 to get the shaded area of the 2x2 square = 2pi-4. Since there are 4 of these little 2x2 squares, multiply the total by 4. = 8pi-16.
the circle is y=sqrt(4-x^2). Sorry foe the typo.
8π−16
In First Image: The radius of the semi circles are 2 . Then the area of a semi circle is 2 π ∗ 2 2 = 2 π . The area of non-red part is 2 ∗ 2 π = 4 π .
The area of red part = (Area of Square − 4 π ) = 1 6 − 4 π
In Second Image: The area of red part = 2 ∗ ( 1 6 − 4 π ) = 3 2 − 8 π
Area of this white part(our desired shaded part)
= ( Area of Square − ( 3 2 − 8 π ) = 1 6 − 3 2 + 8 π = 8 π − 1 6