Beauty of Geometry - 1
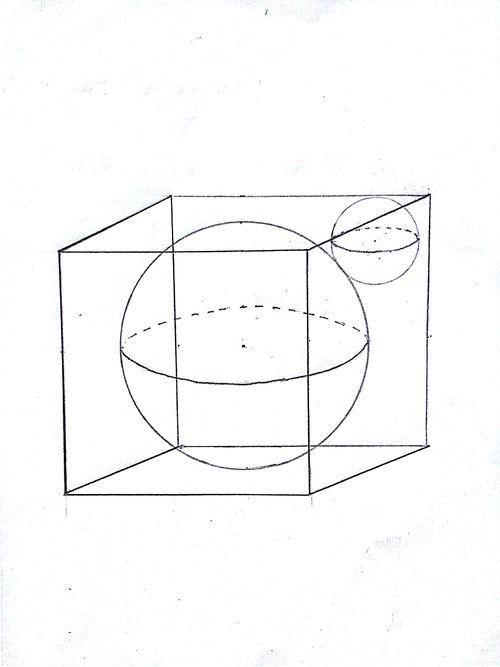 There is a sphere inscribed in a cube. Inside the cube, where the inscribed sphere isn't present, we inscribe another small sphere touching both of the cube and the bigger sphere.
There is a sphere inscribed in a cube. Inside the cube, where the inscribed sphere isn't present, we inscribe another small sphere touching both of the cube and the bigger sphere.
If the radius of the bigger sphere is 17 cm, then what will be the radius of the smaller sphere (in cm)? Round your answer to 3 decimal digit.
The answer is 4.555.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the bigger and smaller sphere be R & r respectively.
Now, cut the cube diagonally in 2 equal halves which goes through the center of both sphere. Then, draw a line from the center of the bigger sphere to that particular corner of the cube which will go through the center of the smaller sphere . Finally, draw two squares as shown in the picture below:
Look closely, the biggest square in the picture is the diagonal slice of the original cube. So, the other two squares which was drawn will also be diagonal slice of two other cubes. As the diagonal of a cube is equal to 3 times it's edge we get, O A + A B + B C = O C ⇒ R + r + 3 r = 3 R ⇒ r = 3 + 1 R ( 3 − 1 ) ⇒ r = R ( 2 − 3 )
So the radius of the smaller circle will be, r = 1 7 ( 2 − 3 ) = 4 . 5 5 5