Beauty of Triangular Basics

Geometry Level 2

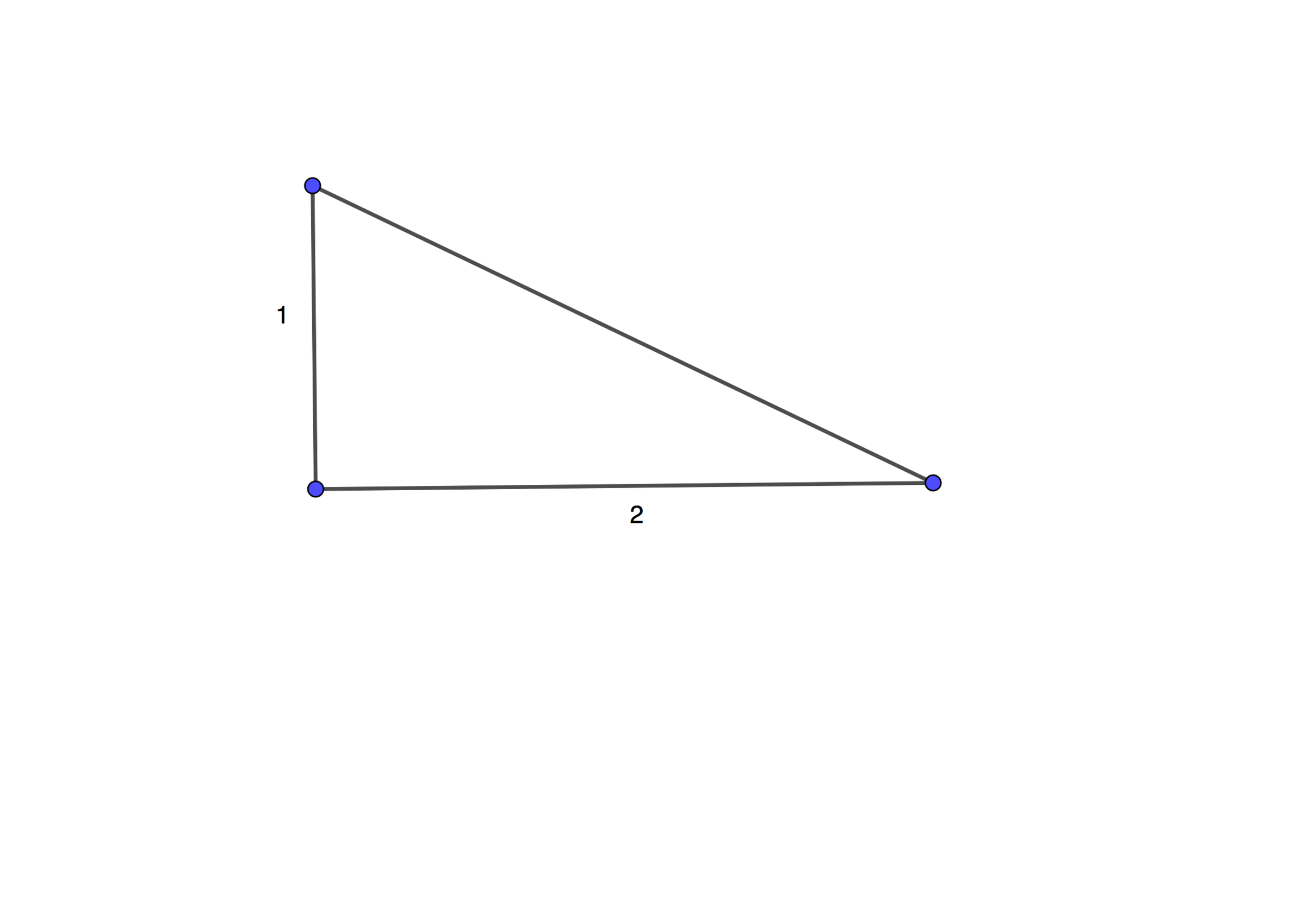
A specific type of triangle has side lengths of 1 and 2, and an angle of 90º. One example of this type of triangle is shown below. In these multiple types of triangles, are the other two angles ever exactly 60º and 30º? Note: The diagram shown below is not drawn to scale. Hint: Go with your intuition, the answer is quite easy!

Yes, but only in 2 cases No, but the ratio of the two angles is always (1+Square root of 5)/2, which is the Golden Ratio! No, but in 1 case, the ratio of the two angles is e:1 Always No, the larger angle is always smaller than twice the smaller angle Yes, but only in 1 case No, the larger angle is always more than twice the smaller anger Never

Winston Choo by Winston Choo , 46, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Winston Choo
Sep 6, 2018

There are only 2 types of such triangles, the one shown above and the one with '2' on the triangle's hypotenuse. Using trigonometry, the first case produced 63º and 27º, while the second case gives a perfect 60º and 30º. Therefore, the answer is: Yes, but only in 1 case .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

You can also say that there are 3 possible triangles: 1 , 2 , s q r t ( 5 ) ; 1 , s q r t ( 3 ) , 2 ; s q r t ( 3 ) , 1 , 2 1,2,sqrt(5);1,sqrt(3),2;sqrt(3),1,2 , and then there are 2 possibilities...

Maurice van Peursem - 2 years, 9 months ago

Log in to reply

Thanks for the note!

Winston Choo - 2 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...